题目内容
17.某校开展“文明小卫士”活动,从学生会“督查部”的3名学生(2男1女)中随机选两名进行督导,恰好选中两名男学生的概率是( )| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好选中两名男学生的情况,再利用概率公式即可求得答案.
解答 解:画树状图得:
∵共有6种等可能的结果,恰好选中两名男学生的有2种情况,
∴恰好选中两名男学生的概率是:$\frac{2}{6}=\frac{1}{3}$.
故选C.
点评 此题考查了树状图法与列表法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
7.下列各对数中,互为相反数的是( )
| A. | -(-3)与|-3| | B. | -(+1)与+(-1) | C. | -23与(-2)3 | D. | -42与(-4)2 |
12.某品牌电脑销售公司有营销员14人,销售部为制定营销人员月销售电脑定额,统计了这14人某月的销售量如下(单位:台):
(1)求这14位营销员该月销售该品牌电脑的平均数、中位数和众数.
(2)销售部经理把每位营销员月销售量定为90台,你认为是否合理?为什么?
| 销售量 | 200 | 170 | 130 | 80 | 50 | 40 |
| 人 数 | 1 | 1 | 2 | 5 | 3 | 2 |
(2)销售部经理把每位营销员月销售量定为90台,你认为是否合理?为什么?
6.同时经过平面三点可确定的直线的条数是( )
| A. | 0 | B. | 0或1 | C. | 1或3 | D. | 3 |
7.下列方程是一元二次方程的是( )
| A. | ax2-2x+=0(a是已知数) | B. | 3x2+2x-4=3x2 | ||
| C. | 5x2-2x=0 | D. | $\frac{{x}^{3}+2x}{x}$=1 |
 尺规作图:如左图,在四边形ABCD内找一点P,使得点P到AB、AD的距离相等,并且点P到点B、C的距离也相等.(不写作法,保留作图痕迹).
尺规作图:如左图,在四边形ABCD内找一点P,使得点P到AB、AD的距离相等,并且点P到点B、C的距离也相等.(不写作法,保留作图痕迹).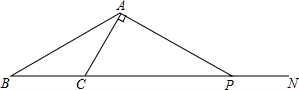 如图,点N是△ABC的边BC延长线上的一点,∠ACN=2∠BAC,过点A作AC的垂线交CN于点P.
如图,点N是△ABC的边BC延长线上的一点,∠ACN=2∠BAC,过点A作AC的垂线交CN于点P.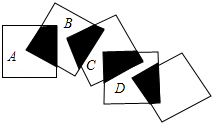 将五个边长都为3cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和是9cm2.
将五个边长都为3cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和是9cm2.