题目内容
1.已知:x=$\frac{1}{\sqrt{2}-1}$,y=$\frac{1}{\sqrt{2}+1}$,求下列各式的值:(1)x2+2xy+y2;
(2)x2-y2;
(3)x2+y2.
分析 (1)先化简x、y的值,然后代入x2+2xy+y2,从而可以解答本题;
(2)先化简x、y的值,然后代入x2-y2,从而可以解答本题;
(3)先化简x、y的值,然后代入x2+y2,从而可以解答本题.
解答 解:(1)∵x=$\frac{1}{\sqrt{2}-1}$=$\sqrt{2}+1$,y=$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}-1$,
x2+2xy+y2
=(x+y)2
=($\sqrt{2}+1+\sqrt{2}-1$)2
=8;
(2)∵x=$\frac{1}{\sqrt{2}-1}$=$\sqrt{2}+1$,y=$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}-1$,
∴x2-y2
=(x+y)(x-y)
=($\sqrt{2}+1+\sqrt{2}-1$)($\sqrt{2}+1-\sqrt{2}+1$)
=$2\sqrt{2}$×2
=4$\sqrt{2}$;
(3)∵x=$\frac{1}{\sqrt{2}-1}$=$\sqrt{2}+1$,y=$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}-1$,
∴x2+y2
=$(\sqrt{2}+1)^{2}+(\sqrt{2}-1)^{2}$
=$3+2\sqrt{2}+3-2\sqrt{2}$
=6.
点评 本题考查二次根式的化简求值,解题的关键是明确二次根式化简求值的方法.

练习册系列答案
相关题目
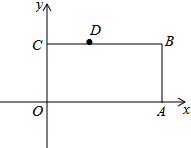 如图,已知长方形OABC的两边分别在x轴、y轴的正半轴上,且点A(4,0),一反比例函数y=$\frac{k}{x}$的图象与边BC交于点D(1,2)
如图,已知长方形OABC的两边分别在x轴、y轴的正半轴上,且点A(4,0),一反比例函数y=$\frac{k}{x}$的图象与边BC交于点D(1,2)
 如图,直线y=-x+b和y=mx+4m(m≠0)的交点的横坐标为-2,则满足不等式组-x+b>mx+4m>0的解集是-4<x<-2.
如图,直线y=-x+b和y=mx+4m(m≠0)的交点的横坐标为-2,则满足不等式组-x+b>mx+4m>0的解集是-4<x<-2.