题目内容
6.已知关于x的方程式:x2-(m+1)x+$\frac{1}{4}$m(m+2)=0(m为常数).(1)求证:无论m取何值,这个方程总有两个不相等的实数根;
(2)解这个方程;
(3)设这个方程的两个根分别为x1、x2,①求证:|x1-x2|=1;②若x1•x2=6,求m的值.
分析 (1)根据根的判别式△=b2-4ac的符号来判定该方程的根的情况;
(2)利用求根公式即可解得结果;
(3)利用根与系数的关系和完全平方公式可得结果.
解答 (1)证明:∵△=[-(m+1)]2-4×$1×\frac{1}{4}$m(m+2)
=1>0,
∴无论m取何值,这个方程总有两个不相等的实数根;
(2)解:x=$\frac{-[-(m+1)]±\sqrt{△}}{2×1}$=$\frac{m+1±1}{2}$,
${x}_{1}=\frac{m+2}{2}$,x2=$\frac{m}{2}$;
(3)x1+x2=m+1,x1•x2=$\frac{1}{4}$m(m+2)
①证明:∵x1-x2=${{(x}_{1}{+x}_{2})}^{2}$-4x1x2
=(m+1)2-4×$\frac{1}{4}$m(m+2)
=1,
∴|x1-x2|=1;
②解:∵x1•x2=6,
∴$\frac{1}{4}$m(m+2)=6,
整理得,m2+2m-24=0,
解得:m=-6或m=4.
点评 本题考查了根与系数的关系、根的判别式.关键是掌握一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
17.a与b互为倒数,则a2016•(-b)2015的值是( )
| A. | a | B. | b | C. | -b | D. | -a |
 如图,等边三角形ABF的顶点F在正五边形ABCDE的内部,则∠CBF=60度.
如图,等边三角形ABF的顶点F在正五边形ABCDE的内部,则∠CBF=60度.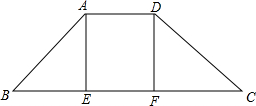 梯形ABCD中,AD∥BC,AE⊥BC于点E,DF⊥BC于点F,∠B=∠C=45°,AD=AE=2,CD=2$\sqrt{2}$,动点P从点C出发以每秒1个单位长度的速度沿这线段CD-DA-AB运动,当点P到达点B时停止运动,运动过程中,点P作BC的垂线与BC交于点Q,设直线PQ扫过梯形ABCD的面积为S,点P运动的时间为t.
梯形ABCD中,AD∥BC,AE⊥BC于点E,DF⊥BC于点F,∠B=∠C=45°,AD=AE=2,CD=2$\sqrt{2}$,动点P从点C出发以每秒1个单位长度的速度沿这线段CD-DA-AB运动,当点P到达点B时停止运动,运动过程中,点P作BC的垂线与BC交于点Q,设直线PQ扫过梯形ABCD的面积为S,点P运动的时间为t.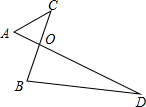 如图,AD与BC相交于点O,$\frac{OA}{OB}$=$\frac{OC}{OD}$,且OA=2,OB=AC=3,求BD的长.
如图,AD与BC相交于点O,$\frac{OA}{OB}$=$\frac{OC}{OD}$,且OA=2,OB=AC=3,求BD的长.