Question

12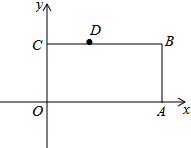．如图，已知长方形OABC的两边分别在x轴、y轴的正半轴上，且点A（4，0），一反比例函数y=$\frac{k}{x}$的图象与边BC交于点D（1，2）
（1）求直线OB函数解析式；
（2）若反比例函数图象上有另一点E，且S_△DBE=9，求点E的坐标．

Answer 1

分析 （1）根据矩形的性质求出点B的坐标，利用待定系数法求出直线OB函数解析式；
（2）根据题意求出反比例函数解析式，根据题意求出点E的纵坐标，代入解析式求出横坐标即可．

解答 解：（1）∵四边形OABC是长方形，点A（4，0），点D（1，2），
∴点B（4，2），
设直线OB函数解析式为：y=kx，
则2=k×4，
解得，k=$\frac{1}{2}$，
则直线OB函数解析式为y=$\frac{1}{2}$x；
（2）∵反比例函数y=$\frac{k}{x}$的图象与边BC交于点D（1，2），
∴k=2，
则反比例函数的解析式为：y=$\frac{2}{x}$，
∵BD=3，S_△DBE=9，
∴点E的纵坐标为6，
则x=$\frac{2}{6}$=$\frac{1}{3}$，
则点E的坐标为（$\frac{1}{3}$，6）．

点评 本题考查的是反比例函数与一次函数的交点问题、矩形的性质，掌握反比例函数图象上点的坐标特点以及矩形的性质是解题的关键．