题目内容
9.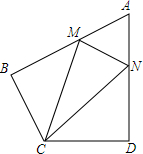 如图,在四边形ABCD中,AB=AD,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,MC=NC,求证:△AMN是等边三角形.
如图,在四边形ABCD中,AB=AD,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,MC=NC,求证:△AMN是等边三角形.
分析 连接AC,可通过HL证明Rt△ABC≌Rt△ADC得到BC=DC,再通过HL证明Rt△MBC≌Rt△NDC得到BM=DN,再根据等量关系得到AM=AN,再根据等边三角形的判定即可证明.
解答 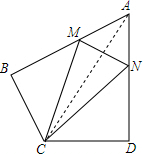 证明:连接AC,
证明:连接AC,
∵AB⊥BC,AD⊥CD,
∴∠B=∠D=90°,
在Rt△ABC与Rt△ADC中,
$\left\{\begin{array}{l}{AB=AD}\\{AC=AC}\end{array}\right.$,
∴Rt△ABC≌Rt△ADC(HL),
∴BC=DC,
在Rt△MBC≌与Rt△NDC中,
$\left\{\begin{array}{l}{BC=DC}\\{MC=NC}\end{array}\right.$,
∴Rt△MBC≌Rt△NDC(HL),
∴BM=DN,
∵AB=AD,
∴AM=AN,
∵∠BAD=60°,
∴△AMN是等边三角形.
点评 考查了等边三角形的判定,全等三角形的判定与性质,关键是根据全等三角形的判定与性质得到AM=AN.

练习册系列答案
相关题目
19.已知菱形ABCD的一边为10cm,则它的周长是( )
| A. | 10cm | B. | 20cm | C. | 30cm | D. | 40cm |

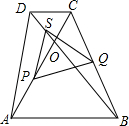 如图,在等腰梯形ABCD中,AB∥DC,AD=BC,对角线AC与BD相交于点O,∠ACD=60°,点S、P、Q分别为OD、OA、BC的中点.
如图,在等腰梯形ABCD中,AB∥DC,AD=BC,对角线AC与BD相交于点O,∠ACD=60°,点S、P、Q分别为OD、OA、BC的中点.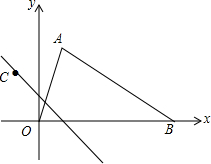 如图,在△AOB中,O是坐标原点,AB=0B,A(1,3),点C在直线y=-x+1上.
如图,在△AOB中,O是坐标原点,AB=0B,A(1,3),点C在直线y=-x+1上.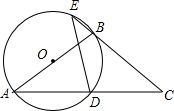 如图,点D是等腰△ABC底边的中点,过点A、B、D作⊙O.
如图,点D是等腰△ABC底边的中点,过点A、B、D作⊙O.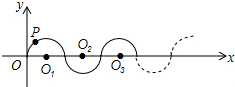 如图,在平面直角坐标系中,半径均为1各单位长度的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第2015秒时,点P的坐标是(2015,-1).
如图,在平面直角坐标系中,半径均为1各单位长度的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第2015秒时,点P的坐标是(2015,-1).