题目内容
12.圆的内接等腰三角形ABC,圆的半径为10,如果底边BC的长为16,那么△ABC的面积为32或128.分析 作AD⊥BC于D,根据等腰三角形的性质得BD=CD=$\frac{1}{2}$BC=8,即AD垂直平分BC,根据垂径定理得到圆心O在AD上;连结OD,在Rt△OBC中利用勾股定理计算出OD=6,然后分类讨论:当△ABC为锐角三角形时,AD=OA+OD=16;当△ABC为钝角三角形时,AD=OA-OD=4,再根据三角形面积公式分别进行计算.
解答 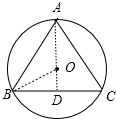 解:作AD⊥BC于D,
解:作AD⊥BC于D,
∵AB=AC,
∴BD=CD=$\frac{1}{2}$BC=8,
∴AD垂直平分BC,
∴圆心O在AD上,连结OB,
在Rt△OBC中,∵BD=8,OB=10,
∴OD=$\sqrt{O{B}^{2}-B{D}^{2}}$=6,
当△ABC为锐角三角形时,AD=OA+OD=10+6=16,此时S△ABC=$\frac{1}{2}$×16×16=128;
当△ABC为钝角三角形时,AD=OA-OD=10-6=4,此时S△ABC=$\frac{1}{2}$×16×4=32.
故答案为:32或128.
点评 本题考查了垂径定理:垂直弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了等腰三角形的性质和勾股定理.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
3.自2016年1月21日开建的印尼雅万高铁是中国和印尼合作的重大标志性项目,这条高铁的总长为152公里.其中“152公里”用科学记数法可以表示为( )
| A. | 0.152×106m | B. | 1.52×105m | C. | 1.52×106m | D. | 152×105m |
2. 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1;…,按这样的规律进行下去,第2016个正方形的面积为( )
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1;…,按这样的规律进行下去,第2016个正方形的面积为( )
 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1;…,按这样的规律进行下去,第2016个正方形的面积为( )
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1;…,按这样的规律进行下去,第2016个正方形的面积为( )| A. | 5×($\frac{3}{2}$)2016 | B. | 5×($\frac{9}{4}$)2016 | C. | 5×($\frac{9}{4}$)2015 | D. | 5×($\frac{3}{2}$)4032 |
 已知:如图,在?ABCD中,M、N分别是AB、CD的中点,AN与DM相交于点P,BN与CM相交于点Q.求证:四边形PMQN是平行四边形.
已知:如图,在?ABCD中,M、N分别是AB、CD的中点,AN与DM相交于点P,BN与CM相交于点Q.求证:四边形PMQN是平行四边形. 如图,已知AB=DC,AC=DB,AC与BD交于一点O,求证:△OBC是等腰三角形.
如图,已知AB=DC,AC=DB,AC与BD交于一点O,求证:△OBC是等腰三角形.
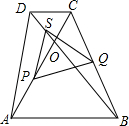 如图,在等腰梯形ABCD中,AB∥DC,AD=BC,对角线AC与BD相交于点O,∠ACD=60°,点S、P、Q分别为OD、OA、BC的中点.
如图,在等腰梯形ABCD中,AB∥DC,AD=BC,对角线AC与BD相交于点O,∠ACD=60°,点S、P、Q分别为OD、OA、BC的中点.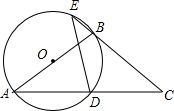 如图,点D是等腰△ABC底边的中点,过点A、B、D作⊙O.
如图,点D是等腰△ABC底边的中点,过点A、B、D作⊙O.