题目内容
 如图,在矩形ABCD中,∠ADC的平分线DF交AC于点E,交BC于点F,∠BDF=15°,求∠DOC和∠COF的度数.
如图,在矩形ABCD中,∠ADC的平分线DF交AC于点E,交BC于点F,∠BDF=15°,求∠DOC和∠COF的度数.考点:矩形的性质
专题:
分析:先根据矩形的性质得出OA=OC=OB=OD,∠ADO=∠OAD=30°,即可得出∠DOC=∠ADO+∠OAD=60°;再证明△OCD是等边三角形,△DCF是等腰三角形,从而证出△OCF是等腰三角形,求出∠COF.
解答:
解:∵四边形ABCD是矩形,
∴∠ADC=∠BCD=90°,OC=OA=
AC,OD=OB=
BD,AC=BD,
∴OA=OC=OB=OD,
∴∠OAD=∠ODA,
∵DF平分∠ADC,
∴∠ADF=∠CDF=45°,
∴∠ADO=∠ADF-∠BDF=45°-15°=30°,∠DFC=45°,
∴∠DOC=30°+30°=60°,∠CDF=∠DFC,
∴△OCD是等边三角形,
∴OC=CD,∠OCD=60°,CD=CF,
∴OC=CF,∠OCF=90°-60°=30°,
∴∠COF=
(180°-30°)=75°.
∴∠ADC=∠BCD=90°,OC=OA=
| 1 |
| 2 |
| 1 |
| 2 |
∴OA=OC=OB=OD,
∴∠OAD=∠ODA,
∵DF平分∠ADC,
∴∠ADF=∠CDF=45°,
∴∠ADO=∠ADF-∠BDF=45°-15°=30°,∠DFC=45°,
∴∠DOC=30°+30°=60°,∠CDF=∠DFC,
∴△OCD是等边三角形,
∴OC=CD,∠OCD=60°,CD=CF,
∴OC=CF,∠OCF=90°-60°=30°,
∴∠COF=
| 1 |
| 2 |
点评:本题考查了矩形的性质、等边三角形的判定与性质研究等腰三角形的判定与性质;证明三角形是等腰三角形和等边三角形是解决问题的关键

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
-2015的相反数是( )
| A、2015 | ||
| B、-2015 | ||
C、
| ||
D、-
|
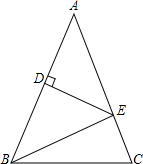 如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,垂足为D,∠EBC:∠EBA=1:2,求∠A的度数.
如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,垂足为D,∠EBC:∠EBA=1:2,求∠A的度数.