题目内容
 某岛O为我国固有领土,对进入该岛12海里范围内的外国船只,我海监船将予以驱离.一天我一艘海监船巡航至岛O正南约14海里的A处,发现在其北偏东45°方向8
某岛O为我国固有领土,对进入该岛12海里范围内的外国船只,我海监船将予以驱离.一天我一艘海监船巡航至岛O正南约14海里的A处,发现在其北偏东45°方向8| 2 |
(1)请你通过计算,求出可疑船在B处时离岛O的距离
(2)求出可疑船驶离时的平均速度(参考数据sin53°≈0.8,cos53°≈0.6,tan53°≈
| 4 |
| 5 |
考点:解直角三角形的应用-方向角问题
专题:
分析:(1)首先利用锐角三角函数关系得出BD,AD的长,再利用勾股定理求出OB的长;
(2)利用锐角三角函数关系得出CD,BC的长进而得出答案.
(2)利用锐角三角函数关系得出CD,BC的长进而得出答案.
解答: 解;(1)过点B作BD⊥AO,交AO于点D,并连接BO,
解;(1)过点B作BD⊥AO,交AO于点D,并连接BO,
由已知,得,AO=14(海里),∠BAD=45°,AB=8
(海里),∠DAC=53°,
∵Rt△ABD中,∠BAD=45°,AB=8
(海里),
∴BD=sin45°•AB=8(海里),
AD=cos45•AB=8(海里),
∴OD=AO-AD=6(海里),
∴Rt△OBD中,OB=
=
=10(海里),
即可疑船在B处时离岛O的距离是10海里;
(2)∵Rt△ADC中,∠DAC=53°,AD=8海里,
∴CD=tan53°•AD≈
(海里),
又∵BD=8(海里),
∴BC=CD-BD=
(海里),
∴可疑船驶离时的平均速度为:
÷
=16(海里/时).
 解;(1)过点B作BD⊥AO,交AO于点D,并连接BO,
解;(1)过点B作BD⊥AO,交AO于点D,并连接BO,由已知,得,AO=14(海里),∠BAD=45°,AB=8
| 2 |
∵Rt△ABD中,∠BAD=45°,AB=8
| 2 |
∴BD=sin45°•AB=8(海里),
AD=cos45•AB=8(海里),
∴OD=AO-AD=6(海里),
∴Rt△OBD中,OB=
| OD2+BD2 |
| 62+82 |
即可疑船在B处时离岛O的距离是10海里;
(2)∵Rt△ADC中,∠DAC=53°,AD=8海里,
∴CD=tan53°•AD≈
| 32 |
| 3 |
又∵BD=8(海里),
∴BC=CD-BD=
| 8 |
| 3 |
∴可疑船驶离时的平均速度为:
| 8 |
| 3 |
| 1 |
| 6 |
点评:此题主要考查了解直角三角形的应用,根据题意熟练应用锐角三角函数关系是解题关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
在Rt△ABC中,∠A=90°,AC=5,BC=13,那么tanB的值是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若等腰三角形的一边长为3cm,另一边长为6cm,则这个三角形的周长为( )
| A、12cm或15cm |
| B、12cm |
| C、15cm |
| D、18cm |
 如图,已知AC∥BD,∠1=55°,则∠2等于( )
如图,已知AC∥BD,∠1=55°,则∠2等于( )| A、125° | B、115° |
| C、135° | D、145° |
 如图,平面上四个点A,B,C,D.按要求完成下列问题:
如图,平面上四个点A,B,C,D.按要求完成下列问题: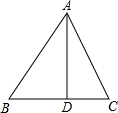 如图,在△ABC中,AD⊥BC,sinB=
如图,在△ABC中,AD⊥BC,sinB=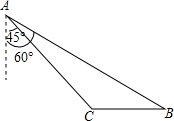 如图所示,2013年4月10日,中国渔民在中国南海huangyandao附近捕鱼作业,中国海监渔船在A第侦察发现,在东南偏东60°方向的B地,有一艘某国军舰正以每小时13海里的速度向正西方方向的C地行驶,企图抓捕正在C地捕鱼的中国渔民.此时,C地位于中国海监船的南偏东45°方向的10海里处,中国海监船以每小时30海里的速度赶往C地救援我国渔民,能不能及时赶到?(
如图所示,2013年4月10日,中国渔民在中国南海huangyandao附近捕鱼作业,中国海监渔船在A第侦察发现,在东南偏东60°方向的B地,有一艘某国军舰正以每小时13海里的速度向正西方方向的C地行驶,企图抓捕正在C地捕鱼的中国渔民.此时,C地位于中国海监船的南偏东45°方向的10海里处,中国海监船以每小时30海里的速度赶往C地救援我国渔民,能不能及时赶到?(