题目内容
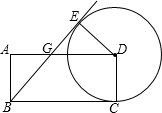 如图,矩形ABCD中,AB=1,BC=3,以D为圆心,CD为半径作⊙D,直线BE切⊙D于点E,BE交AD于点G,则AG=
如图,矩形ABCD中,AB=1,BC=3,以D为圆心,CD为半径作⊙D,直线BE切⊙D于点E,BE交AD于点G,则AG=考点:切线的性质,矩形的性质
专题:计算题
分析:先根据矩形的性质得CD=AB=1,AD=BCV=3,再根据切线的性质得DE⊥BE,DE=DC=1,则DE=AB,于是可证明△DEG≌△BAG,得到DG=BG,设AG=x,则DG=BG=3-x,然后在Rt△ABG中利用勾股定理得12+x2=(3-x)2,再解方程求出x即可.
解答:解:∵四边形ABCD为矩形,
∴CD=AB=1,AD=BCV=3,
∵直线BE切⊙D于点E,
∴DE⊥BE,
∴∠DEG=90°,DE=DC=1,
∴DE=AB,
在△DEG和△BAG中,
,
∴△DEG≌△BAG(AAS),
∴DG=BG,
设AG=x,则DG=AD-AG=3-x,BG=3-x,
在Rt△ABG中,∵AB2+AG2=BG2,
∴12+x2=(3-x)2,解得x=
,
即AG=
.
故答案为
.
∴CD=AB=1,AD=BCV=3,
∵直线BE切⊙D于点E,
∴DE⊥BE,
∴∠DEG=90°,DE=DC=1,
∴DE=AB,
在△DEG和△BAG中,
|
∴△DEG≌△BAG(AAS),
∴DG=BG,
设AG=x,则DG=AD-AG=3-x,BG=3-x,
在Rt△ABG中,∵AB2+AG2=BG2,
∴12+x2=(3-x)2,解得x=
| 4 |
| 3 |
即AG=
| 4 |
| 3 |
故答案为
| 4 |
| 3 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了勾股定理、全等三角形的判定与性质.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 如图,在矩形ABCD中,AB=2,BC=4,⊙D的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心O重合,绕着O点转动三角板,使它的一条直角边与⊙D切于点H,此时两直角边与AD交于E,F两点,则tan∠EFO的值为( )
如图,在矩形ABCD中,AB=2,BC=4,⊙D的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心O重合,绕着O点转动三角板,使它的一条直角边与⊙D切于点H,此时两直角边与AD交于E,F两点,则tan∠EFO的值为( )| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
 如图,A、B、C、D在同一条直线上,∠EAD=∠FAD,∠EDA=∠FDA,则图中共有全等三角形( )
如图,A、B、C、D在同一条直线上,∠EAD=∠FAD,∠EDA=∠FDA,则图中共有全等三角形( )| A、3对 | B、4对 | C、5对 | D、6对 |
不等式组
的解集在数轴上表示正确的是( )
|
A、 |
B、 |
C、 |
D、 |
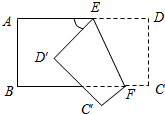 如图,把一张长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠AED′=50°,则∠EFB等于( )
如图,把一张长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠AED′=50°,则∠EFB等于( )| A、50° | B、55° |
| C、60° | D、65° |
甲、乙两人进行射击比赛,在相同条件下各射击10次,他们的平均成绩为7环,10次射击成绩的方差分别是:S2甲=3,S2乙=1.2,成绩较稳定的是( )
| A、甲 | B、乙 |
| C、一样稳定 | D、无法确定 |
 如图,直线AB、CD相交于O,且∠AOC:∠BOC=1:2,∠AOF=∠BOF=90°,OE平分∠BOC,求:∠EOF的度数.
如图,直线AB、CD相交于O,且∠AOC:∠BOC=1:2,∠AOF=∠BOF=90°,OE平分∠BOC,求:∠EOF的度数.


