题目内容
13.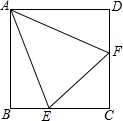 在正方形ABCD中,E是BC边上的点,F是CD边上的点,且AE=AF,AB=4,设△AEF的面积为y,EC为长为x
在正方形ABCD中,E是BC边上的点,F是CD边上的点,且AE=AF,AB=4,设△AEF的面积为y,EC为长为x(1)求y关于x的函数表达式;
(2)当△AEF为正三角形时,求△AEF的面积.
分析 (1)根据AB,CE长度,利用S△AEF=16-S△ABE-S△ADF-S△CE即可解决.
(2)根据△AEF为正三角形时得∠BAE=15°,在AB上取一点M使得AM=ME,则∠MAE=∠AEM=15°,所以∠BME=30°,设BE=a,则AM=ME=2a,BM=4-2xa,在RT△MBE利用勾股定理即可求出a,进而得出EC,再利用(1)结论计算.
解答 解:(1)在RT△ABE和RT△ADF中,
$\left\{\begin{array}{l}{AD=AB}\\{AE=AF}\end{array}\right.$,
∴RT△ABE≌RT△ADF(HL),
∴BE=DF,
∵CE=x,AB=BC=CD=4
∴BE=4-x,
∴S△AEF=16-S△ABE-S△ADF-S△CEF
y=16-$\frac{1}{2}$×4×(4-x)-$\frac{1}{2}$×4×(4-x)-$\frac{1}{2}$x2
=-$\frac{1}{2}$x2+4x.
(2)∵△AEF是等边三角形,
∴∠EAF=60°,
∵RT△ABE≌RT△ADF,∠BAD=90° ∴∠BAE=∠DAF=15°,在AB上取一点M使得AM=ME,则∠MAE=∠AEM=15°,
∴∠BAE=∠DAF=15°,在AB上取一点M使得AM=ME,则∠MAE=∠AEM=15°,
∴∠BME=30°,
设BE=a,则AM=ME=2a,BM=4-2xa,
在RT△MBE中,∵BM2+BE2=ME2,
∴(4-2a)2+a2=(2a)2,
∴a=8-4$\sqrt{3}$(或8+4$\sqrt{3}$不合题意舍弃)
∴x=EC=4-(8-4$\sqrt{3}$)=4$\sqrt{3}$-4
把x=4$\sqrt{3}$-4代入y=-$\frac{1}{2}$x2+4x得y=32$\sqrt{3}$-48,
∴△AEF的面积为32$\sqrt{3}$-48.
点评 本题考查正方形的性质、直角三角形中30度角的性质勾股定理等知识,解题的关键是15度角如何转化为30度角,属于中考常考题型.

 名校课堂系列答案
名校课堂系列答案| A. | 6 | B. | ±6 | C. | 12 | D. | ±12 |
| A. | -(-2x+3)=2x-3 | B. | -(2x-3)=2x+3 | C. | -(-2x-3)=-2x+3 | D. | -(2x+3)=-2x+3 |
| 成本P(元/kg) | 8-$\frac{x}{10}$ |
| 销售量q(kg) | 1000-10x |
(2)设该种植户每天获得的利润为y(元),求y关于x的函数关系式,指出第几天获得的利润最大,最大值是多少?
(3)该种植户决定,每销售1kg水果就捐出m(m≤2)元,满足每天获得的利润随x的增大而增大,求m的取值范围.

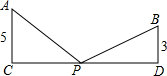 如图,A、B两个工厂合用的一个变压器位于P处,两厂位于过P的笔直高压输电线的同一侧,P到A、B两厂的距离相等,A、B两厂到高压线的距离分别为AC、BD,且AC=5千米,BD=3千米.如果CD=16千米,那么变压器所在处P与C处的距离是多少千米?
如图,A、B两个工厂合用的一个变压器位于P处,两厂位于过P的笔直高压输电线的同一侧,P到A、B两厂的距离相等,A、B两厂到高压线的距离分别为AC、BD,且AC=5千米,BD=3千米.如果CD=16千米,那么变压器所在处P与C处的距离是多少千米?