题目内容
1.下列图形按一定规律排列,观察并回答:
(1)依照此规律,第四个图形的★共有13个,第六个图形的★共有19个;
(2)第n个图形的★有3n+1个;
(3)问是否存在连续3个图形恰好共有300个★?
分析 (1)根据已知三个图形中★数量可知,每一个图形中★的数量是序数的3倍与1的和,据此规律可知第4、6个图形中★的数量;
(2)由(1)中规律列代数式即可;
(3)可分别设连续3个图形分别是第n,n+1,n+2个图形,将每个图形中★的数量相加,可列出方程,解方程可得.
解答 解:(1)根据题意知,
∵第一个图形中★的个数为:1+3×1=4个;
第二个图形中★的个数为:1+3×2=7个;
第三个图形中★的个数为:1+3×3=10个;
∴第四个图形中★的个数为:1+3×4=13个;
第六个图形中★的个数为:1+3×6=19个;
(2)由(1)规律可知,第n个图形中★的个数为:1+3×n=3n+1个;
(3)设连续3个图形分别是第n,n+1,n+2个图形,
根据题意,得:3n+1+3n+4+3n+7=300,
解得:n=32,
答:第32,33,34个图形恰好共有300个★.
故答案为:(1)13,19;(2)3n+1.
点评 本题主要考查图形的变化规律和方程的应用,在图形的变化中善于发现变化和不变的部分是寻求规律的关键,根据题意列方程是方程应用的基本.

练习册系列答案
相关题目
11.下列说法正确的是( )
| A. | 单项式a的次数为0 | B. | 单项式a的系数为0 | ||
| C. | 多项式a4+a2的次数为6 | D. | 单项式πr2的次数为2 |
16.在数轴上,点A(表示整数a)在原点的左侧,点B(表示整数b)在原点的右侧.若|a-b|=44,且AO=3BO,则a+b的值为( )
| A. | -44 | B. | -22 | C. | -55 | D. | -11 |
6.为了解长城小区“全民健身”活动的开展情况,随机对该小区的40名居民一周的体育锻炼时间进行了统计,结果如表:
这40名居民一周体育锻炼时间的中位数是5小时.
| 锻炼时间(时) | 3 | 4 | 5 | 6 | 7 |
| 人数(人) | 6 | 13 | 14 | 5 | 2 |
10.在下面给出的条件中,能判定四边形ABCD是平行四边形的是( )
| A. | AB=BC,AD=DC | B. | AB∥CD,AD=CB | C. | OA=OC,OB=OD | D. | AC=BD,AC⊥BD |
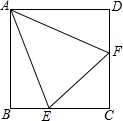 在正方形ABCD中,E是BC边上的点,F是CD边上的点,且AE=AF,AB=4,设△AEF的面积为y,EC为长为x
在正方形ABCD中,E是BC边上的点,F是CD边上的点,且AE=AF,AB=4,设△AEF的面积为y,EC为长为x