题目内容
17.小明和小红在一本数学资料书上看到有这样一道竞赛题:“已知△ABC的三边长分别为a、b、c(a>b),且满足(b+c-2a)2+|b+c-8|=0,求c的取值范围”.(1)小明说:“c的取值范围,我看不出如何求,但我能求出a的长度.”你知道小明是如何计算的吗?你帮他写出求解的过程.
(2)小红说:“我也看不出如何求c的范围,但我能用含c的代数式表示b”.同学,你能吗?若能,帮小红写出过程.
(3)小明和小红一起去问数学老师,老师说:“根据你们二人的求解,利用书上三角形的三边满足的关系,即可求出答案.”你知道答案吗?请写出过程.
分析 (1)利用偶次方以及绝对值的性质化简求出即可;
(2)利用b+c-8=0进而求出即可;
(3)利用三角形三边关系分别得出即可.
解答 解:(1)由题意得:
$\left\{\begin{array}{l}{b+c-2a=0}\\{b+c-8=0}\end{array}\right.$,
则a=4;
(2)由b+c-8=0得:
b=8-c;
(3)由三角形三边关系a+b>c可得
4+8-c>c,
解之得:6>c,
又因为:a>b,即b<4,
∵b+c=8
∴c>4,
故4<c<6.
点评 此题主要考查了二元一次方程组的应用以及偶次方以及绝对值的性质等知识,根据三角形三边关系得出是解题关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
8. 如图是由5个形状、大小完全相同的正六边形组成的图案,我们把正六边形的顶点称为格点.若Rt△ABC的顶点都在格点上,且AB为Rt△ABC的斜边,则Rt△ABC的个数有( )
如图是由5个形状、大小完全相同的正六边形组成的图案,我们把正六边形的顶点称为格点.若Rt△ABC的顶点都在格点上,且AB为Rt△ABC的斜边,则Rt△ABC的个数有( )
 如图是由5个形状、大小完全相同的正六边形组成的图案,我们把正六边形的顶点称为格点.若Rt△ABC的顶点都在格点上,且AB为Rt△ABC的斜边,则Rt△ABC的个数有( )
如图是由5个形状、大小完全相同的正六边形组成的图案,我们把正六边形的顶点称为格点.若Rt△ABC的顶点都在格点上,且AB为Rt△ABC的斜边,则Rt△ABC的个数有( )| A. | 2个 | B. | 4个 | C. | 6个 | D. | 8个 |
5.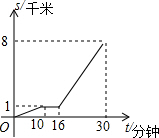 小亮从家步行到公交站台,等公交去学校,图中的折线表示小亮的行程s(千米)与所花时间t(分钟)之间的函数关系.下列说法错误的是( )
小亮从家步行到公交站台,等公交去学校,图中的折线表示小亮的行程s(千米)与所花时间t(分钟)之间的函数关系.下列说法错误的是( )
 小亮从家步行到公交站台,等公交去学校,图中的折线表示小亮的行程s(千米)与所花时间t(分钟)之间的函数关系.下列说法错误的是( )
小亮从家步行到公交站台,等公交去学校,图中的折线表示小亮的行程s(千米)与所花时间t(分钟)之间的函数关系.下列说法错误的是( )| A. | 小亮行程8千米,共用了30分钟 | B. | 小亮等公交车时间为6分钟 | ||
| C. | 小亮步行的速度是100米/分钟 | D. | 公交车的速度是350米/分钟 |
12.正方形和下列边长相同的正多边形地砖组合中,不能够铺满地面的是( )
| A. | 正三角形 | B. | 正六边形 | ||
| C. | 正八边形 | D. | 正三角形和正六边形 |
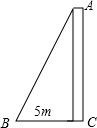 如图,小明想知道学校旗杆的高度,他把升旗绳子一端挂在旗杆顶端,发现绳子垂到地面时还余1m;当他把绳子下端拉开5m后,绳子下端刚好接触到地面,则旗杆高度为12m.
如图,小明想知道学校旗杆的高度,他把升旗绳子一端挂在旗杆顶端,发现绳子垂到地面时还余1m;当他把绳子下端拉开5m后,绳子下端刚好接触到地面,则旗杆高度为12m.
 如图所示,在正方形ABCD中,三角形ADE绕点A顺时针旋转一定角度后与三角形ABF重合,则∠FAE=90度.
如图所示,在正方形ABCD中,三角形ADE绕点A顺时针旋转一定角度后与三角形ABF重合,则∠FAE=90度. 如图,已知∠AOB=60°,点P在边OA上,OP=20,点M,N在边OB上,PM=PN.若MN=6,则OM=( )
如图,已知∠AOB=60°,点P在边OA上,OP=20,点M,N在边OB上,PM=PN.若MN=6,则OM=( )