题目内容
8．
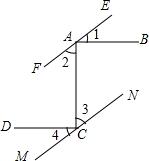已知，如图，EF∥MN，且∠1=∠2，∠3=∠4，求证：AB∥CD．
分析 根据EF∥MN，判断出∠2=∠3，再用条件等量代换得出∠1+∠2=∠3+∠4，进而得出∠BAC=∠DCA即可．
解答 解：∵EF∥MN，
∴∠2=∠3，
∵∠1=∠2，∠3=∠4，
∴∠1=∠2=∠3=∠4，
∴∠1+∠2=∠3+∠4，
∵∠BAC=180°-（∠1+∠2），∠DCA=180°-（∠3+∠4），
∴∠BAC=∠DCA，
∴AB∥CD．
点评 此题是平行线的判定与性质题，还用到了平角的定义，等量代换，解本题的关键是要分析出∠BAC=∠DCA的方法．
练习册系列答案
相关题目
16．下列计算：（1）34÷35=$\frac{1}{3}$；（2）（$\frac{1}{2012}$）0=（-2012）0；（3）（a-2）5÷（a-5）2=1；（4）x4÷x9=x-5，其中正确的有（ ）
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
3．已知点P（x，|x|），则点P一定（ ）
| A． | 在第一象限 | B． | 不在y轴上 | C． | 在x轴上方 | D． | 不在x轴下方 |
13．下列实数中，属于无理数的是（ ）
| A． | -$\frac{1}{3}$ | B． | 0.1 | C． | $\sqrt{4}$ | D． | $\root{3}{9}$ |
20．下列各式是最简二次根式的是（ ）
| A． | $\sqrt{{m}^{2}+1}$ | B． | $\sqrt{a{b}^{5}}$ | C． | $\sqrt{12}$ | D． | $\sqrt{\frac{1}{3}}$ |
17．
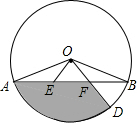如图，AB是⊙O的弦，OA=10，F是线段AB上的点，且FB=FO，OF的延长线交⊙O于点D，∠B=30°，则阴影部分的面积为（ ）
如图，AB是⊙O的弦，OA=10，F是线段AB上的点，且FB=FO，OF的延长线交⊙O于点D，∠B=30°，则阴影部分的面积为（ ）| A． | 25π-$\frac{100\sqrt{3}}{3}$ | B． | 25π-$\frac{50\sqrt{3}}{3}$ | C． | 30π-$\frac{25\sqrt{3}}{2}$ | D． | 20π-$\frac{50\sqrt{3}}{3}$ |