题目内容
10.请阅读下列材料:
问题:如图1,△ABC中,∠ACB=90°,AC=BC,MN是过点A的直线,DB⊥MN于点D,联结CD.求证:BD+AD=$\sqrt{2}$CD.
小明的思考过程如下:要证BD+AD=$\sqrt{2}$CD,需要将BD,AD转化到同一条直线上,可以在MN上截取AE=BD,并联结EC,可证△ACE和△BCD全等,得到CE=CD,且∠ACE=∠BCD,由此推出△CDE为等腰直角三角形,可知DE=$\sqrt{2}$CD,于是结论得证.
小聪的思考过程如下:要证BD+AD=$\sqrt{2}$CD,需要构造以CD为腰的等腰直角三角形,可以过点C作CE⊥CD交MN于点E,可证△ACE和△BCD全等,得到CE=CD,且AE=BD,由此推出△CDE为等腰直角三角形,可知DE=$\sqrt{2}$CD,于是结论得证.
请你参考小明或小聪的思考过程解决下面的问题:
(1)将图1中的直线MN绕点A旋转到图2和图3的两种位置时,其它条件不变,猜想BD,AD,CD之间的数量关系,并选择其中一个图形加以证明;
(2)在直线MN绕点A旋转的过程中,当∠BCD=30°,BD=$\sqrt{2}$时,求CD的长度.
分析 (1)过点C作CE⊥CB于点C,与MN交于点E,证明△ACE≌△DCB,则△ECB为等腰直角三角形,据此即可得到BE=$\sqrt{2}$CB,根据BE=AB-AE即可证得;
(2)过点B作BH⊥CD于点H,证明△BDH是等腰直角三角形,求得DH的长,在直角△BCH中,利用直角三角形中30°的锐角所对的直角边等于斜边的一半,即可求得.
解答 解:(1)如图2,BD-AD=$\sqrt{2}$CD.
如图3,AD-BD=$\sqrt{2}$CD.
证明图2:如图2,在直线MN上截取AE=BD,联结CE.设AC与BD相交于点F,
∵BD⊥MN,
∴∠ADB=90°,
∴∠CAE+∠AFD=90°.
∵∠ACB=90°,∴∠1+∠BFC=90°.
∵∠AFD=∠BFC,∴∠CAE=∠1.
在△ACE和△BCD中
$\left\{\begin{array}{l}{AE=BD}\\{∠CAE=∠1}\\{AC=BC}\end{array}\right.$,
∴△ACE≌△BCD(SAS).
∴CE=CD,∠ACE=∠BCD.
∴∠ACE-∠ACD=∠BCD-∠ACD,即∠2=∠ACB=90°.
在Rt△CDE中,∵CD2+CE2=DE2,
∴2CD2=DE2,即DE=$\sqrt{2}$CD.
∵DE=AE-AD=BD-AD,
∴BD-AD=$\sqrt{2}$CD.
证明:如图3:( 法一)在直线MN上截取AE=BD,联结CE.
设AD与BC相交于点F,∵∠ACB=90°,∴∠2+∠AFC=90°.
∵BD⊥MN,∴∠ADB=90°,∠3+∠BFD=90°.
∵∠AFC=∠BFD,∴∠2=∠3.
在△ACE和△BCD中
$\left\{\begin{array}{l}{AE=BD}\\{∠2=∠3}\\{AC=BC}\end{array}\right.$,
∴△ACE≌△BCD(SAS).
∴CE=CD,∠1=∠4.
∴∠1+∠BCE=∠4+∠BCE,即∠ECD=∠ACB=90°.
在Rt△CDE中,∵CD2+CE2=DE2,
∴2CD2=DE2,即DE=$\sqrt{2}$CD.
∵DE=AD-AE=AD-BD,∴AD-BD=$\sqrt{2}$CD.
如图3,过点C作CE⊥CD交MN于点E,则∠DCE=90°.
∵∠ACB=90°,
∴∠ACB-∠ECB=∠DCE-∠ECB,即∠1=∠4.
设AD与BC相交于点F,
∵DB⊥MN,
∴∠ADB=90°.
∴∠2+∠AFC=90°,∠3+∠BFD=90°.
∵∠AFC=∠BFD,
∴∠2=∠3.
∵∠1+∠ECF=90°,∠ECF+∠4=90°,
∴∠1=∠4,
在△ACE和△BCD中
$\left\{\begin{array}{l}{∠2=∠3}\\{AC=BC}\\{∠1=∠4}\end{array}\right.$,
∴△ACE≌△BCD(ASA).
∴CE=CD,AE=BD.
在Rt△CDE中,CD2+CE2=DE2,
∴2CD2=DE2,即DE=$\sqrt{2}$CD.
∵DE=AD-AE=AD-BD,
∴AD-BD=$\sqrt{2}$CD.
(2)MN在绕点A旋转过程中,这个的意思并没有指明是哪种情况,
∴综合了第一个图和第二个图两种情况
若是第1个图:易证△ACE≌△DCB,CE=CD,
∴△ECD为等腰直角三角形,
∴∠AEC=45°=∠CBD,
如图4,过D作DH⊥CB.则△DHB为等腰直角三角形.
BD=$\sqrt{2}$BH,
∴BH=DH=1.
直角△CDH中,∠DCH=30°,
BH=1,则CH=$\sqrt{3}$.
∴CD=$\sqrt{3}$+1
若是第二个图:如图5,过B作BH⊥CD交CD延长线于H.
解法类似上面,CH=$\sqrt{3}$,DH=1,CD=$\sqrt{3}$-1.
故CD为:$\sqrt{3}$±1.
点评 本题考查了全等三角形的性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的性质是全等三角形的对应边相等,对应角相等.

 阅读快车系列答案
阅读快车系列答案 如图,立体图形的俯视图是( )
如图,立体图形的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
| A. | -6 | B. | 6 | C. | -$\frac{1}{6}$ | D. | $\frac{1}{6}$ |
| A. | 90° | B. | 180° | C. | 270° | D. | 300° |

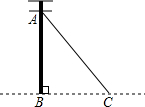 如图,AC是电杆AB的一根拉线,测得BC=6,tan∠ACB=$\frac{4}{3}$,则拉线AC的长为10.
如图,AC是电杆AB的一根拉线,测得BC=6,tan∠ACB=$\frac{4}{3}$,则拉线AC的长为10. 学校操场旁边一棵水杉树被大风吹断,如图测得树顶与水平地面刚好成60度夹角,且离树的底端5米,求这棵树原来有多高?(结果保留整数,$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
学校操场旁边一棵水杉树被大风吹断,如图测得树顶与水平地面刚好成60度夹角,且离树的底端5米,求这棵树原来有多高?(结果保留整数,$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)