题目内容
5.如图,四边形ABCD是矩形,将一块正方形纸板OEFG如图1摆放,它的顶点O与矩形ABCD的对角线交点重合,点A在正方形的边OG上,现将正方形绕点O逆时针旋转,当点B在OG边上时,停止旋转,在旋转过程中OG交AB于点M,OE交AD于点N.(1)开始旋转前,即在图1中,连接NC.
①求证:NC=NA(M);
②若图1中NA(M)=4,DN=2,请求出线段CD的长度.
(2)在图2(点B在OG上)中,请问DN、AN、CD这三条线段之间有什么数量关系?写出结论,并说明理由.
(3)试探究图3中AN、DN、AM、BM这四条线段之间有什么数量关系?写出结论,并说明理由.

分析 (1)①由矩形的对角线互相平分和正方形的内角都是直角,用线段垂直平分线上的点到两端点的距离相等,②用勾股定理计算即可;
(2)和(1)一样得到NB=ND,在用勾股定理即可;
(3)先判断出BM=DH,再和前两个一样,得出MN=NH,再用勾股定理即可.
解答 解:(1)①∵四边形ABCD是矩形,
∴OA=OC,
∵四边形EFGO为正方形,
∴∠EOG=90°,
∴NC=NA;
②由①得,NA=NC=4,DN=2,
根据勾股定理得CD2=NC2-ND2,
∴CD=$\sqrt{16-4}$=2$\sqrt{3}$;
(2)结论:NB2=NA2+CD2,
如图1,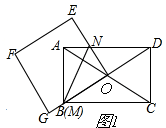
连接NB,
∵四边形ABCD是矩形,
∴OB=OD,AB=CD,
∵四边形EFGO为正方形,
∴∠EOG=90°,
∴ND=NB;
根据勾股定理得,NB2=NA2+AB2=NA2+CD2,
(3)结论AN2+AM2=DN2+BM2,
如图2,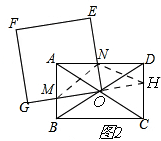
延长GO交CD于H,连接MN,HN,
∵四边形ABCD是矩形,
∴OB=OD,∠OBM=∠ODH,
∵∠BOM=∠DOH,
∴△BOM≌△DOH,
∴BM=DH,OM=OH
∵四边形EFGO是正方形,
∴∠EOG=90°,
∴MN=MH,在Rt△NDH中,
NH2=DN2+DH2=DN2+BM2,
在Rt△AMN中,MN2=AM2+AN2,
∴DN2+BM2=AM2+AN2.
点评 此题是四边形综合题,主要考查了正方形和矩形的性质,勾股定理,线段垂直平分线的性质,解本题的关键是线段垂直平分线的性质定理得应用.

练习册系列答案
相关题目
10.反比例函数y=$\frac{1-6t}{x}$的图象与直线y=-x+2有两个交点,且两交点横坐标的积为负数,则t的取值范围是( )
| A. | t<$\frac{1}{6}$ | B. | t>$\frac{1}{6}$ | C. | t≤$\frac{1}{6}$ | D. | t≥$\frac{1}{6}$ |
7.下列四个几何体中,左视图为圆的几何体是( )
| A. |  | B. |  | C. |  | D. |  |

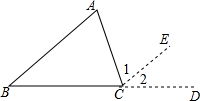 叙述三角形内角和定理并将证明过程填写完整.
叙述三角形内角和定理并将证明过程填写完整.