题目内容
18．
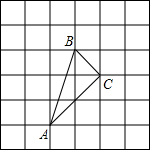如图，小正方形的边长为1，△ABC的三个顶点都在小正方形的顶点处，判断△ABC的形状，并求出△ABC的面积．
分析 利用勾股定理列式求出AB、BC、AC，再根据勾股定理逆定理判断△ABC的形状，根据三角形面积公式求出△ABC的面积．
解答 解：由勾股定理得，AB=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$，
BC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$，
AC=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$，
∵AB2=BC2+AC2，
∴△ABC是直角三角形；
∴△ABC的面积为2$\sqrt{2}$×$\sqrt{2}$÷2=2．
点评 本题考查了勾股定理，勾股定理逆定理，三角形的面积，熟练掌握网格结构并准确找出对应点的位置是解题的关键．
练习册系列答案
相关题目
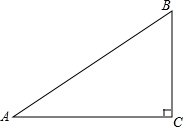如图，在△ABC中，∠C=90°，AC=8，BC=6，D是AB的中点，点E在边AC上，将△ADE沿DE翻折，使得点A落在点A'处，当A'E⊥AC时，A'B=$\sqrt{2}$或7$\sqrt{2}$．
如图，在平面直角坐标系中，点O是坐标原点，四边形ABCO是菱形，点A的坐标为（-3，4），点C在x轴的正半轴上，直线AC交y轴于点M，AB边交y轴于点H，点P是线段AB上的一动点（包括点A，B），且点P的坐标为（a，4）．
如图，在等腰Rt△ABC中，AB=BC；AD平分∠BAC交BC边于点D，点E是AD边上靠近端点A的一动点，以AE为边往上作等腰Rt△AEF，且AE=EF，延长FE交AC于点G；点M为FC中点，连接BM、EM、BE、DM；则下列5个结论：①FA=FG；②△ABD与△ACD的面积比为1：$\sqrt{2}$；③AC=（$\sqrt{2}$+1）BD；④∠MDC=90°；⑤△BME为等腰三角形，但不一定为直角三角形，其中正确的有（ ）个．
18．根据下列条件，能列出方程的是（ ）
| A． | 甲数的3倍与乙数的$\frac{1}{2}$的和 | B． | a与1的差的$\frac{1}{4}$ | ||
| C． | 一个数的2倍比3小1 | D． | a与b的和的$\frac{3}{5}$ |