题目内容
9.在学习概率知识的课堂上,老师组织小组讨论一道题目:在一个不透明的袋子中装有4个除颜色外完全相同的小球,其中白球1个,黄球1个,红球2个,要求同学们按两种规则摸球,规则一:搅匀后从中摸出一个球,放回搅匀后再摸出第二个球;规则二:搅匀后从中一次任意摸出两个球,请你通过画树状图或列表法计算说明哪种规则摸出两个红球的概率较大?分析 列举出所有情况,看两次都摸到红球的情况占总情况的多少即可知道哪种方法摸到两个红球的概率较大.
解答 解:规则一、摸出一个球后放回,再摸出一个球时, ,
,
共有16种等可能的结果数,其中两个都是红球的占4种,
所以两次都摸到红球的概率=$\frac{1}{4}$;
规则二、一次性摸两个球时,
∴一共有12种情况,有2种情况两次都摸到红球,
∴两次都摸到红球的概率是=$\frac{1}{6}$.
∵$\frac{1}{4}$>$\frac{1}{6}$,
∴第一规则摸出两个红球的概率较大.
点评 本题考查了列表法与树状图法,列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.若一次函数y=(2-m)x-4的图象经过点A(x1,y1)和点B(x2,y2),当x1<x2时,y1>y2,则m的取值范围是( )
| A. | m<2 | B. | m>2 | C. | m≤2 | D. | m≥2 |
4.罗山西亚丽宝超市第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的$\frac{1}{2}$倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价-进价)
(1)罗山西亚丽宝超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品.其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?
| 甲 | 乙 | |
| 进价(元/件) | 20 | 30 |
| 售价(元/件) | 29 | 40 |
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品.其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?
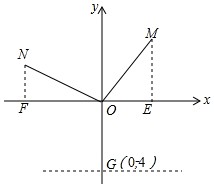 如图,在直角坐标系中,已知点M(2,3),连接OM,在第二象限作N,使ON⊥OM且ON=OM,y轴上有一点G(0,-4),过G作x轴的平行线l.
如图,在直角坐标系中,已知点M(2,3),连接OM,在第二象限作N,使ON⊥OM且ON=OM,y轴上有一点G(0,-4),过G作x轴的平行线l. 如图,等腰直角三角形ABC中,AB=4cm.点D是BC边上的动点,以AD为直角边作等腰直角三角形ADE.在点D从点B移动至点C的过程中,点E移动的路线长为4$\sqrt{2}$cm.
如图,等腰直角三角形ABC中,AB=4cm.点D是BC边上的动点,以AD为直角边作等腰直角三角形ADE.在点D从点B移动至点C的过程中,点E移动的路线长为4$\sqrt{2}$cm. 如图,已知四点A、B、C、D,请用尺规作图完成.(保留画图痕迹)
如图,已知四点A、B、C、D,请用尺规作图完成.(保留画图痕迹)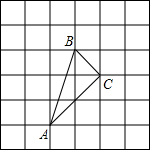 如图,小正方形的边长为1,△ABC的三个顶点都在小正方形的顶点处,判断△ABC的形状,并求出△ABC的面积.
如图,小正方形的边长为1,△ABC的三个顶点都在小正方形的顶点处,判断△ABC的形状,并求出△ABC的面积.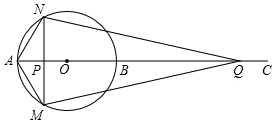 已知:如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以1cm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为2,AC=10,设运动时间为ts.
已知:如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以1cm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为2,AC=10,设运动时间为ts.