题目内容
6.先化简,再求值:$\frac{x}{{x}^{2}-2x+1}$÷($\frac{x+1}{{x}^{2}-1}$+1),其中x=2.分析 首先把括号内的分式通分相加,然后把出发转化为乘法,分子和分母分解因式,然后计算乘法即可化简,然后解方程求得x的值代入求解.
解答 解:原式=$\frac{x}{(x-1)^{2}}$÷$\frac{x+1+({x}^{2}-1)}{{x}^{2}-1}$
=$\frac{x}{(x-1)^{2}}$÷$\frac{x+{x}^{2}}{(x+1)(x-1)}$
=$\frac{x}{(x-1)^{2}}$÷$\frac{x}{x-1}$
=$\frac{x}{(x-1)^{2}}$•$\frac{x-1}{x}$
=$\frac{1}{x-1}$.
当x=2时,原式=$\frac{1}{2-1}$=1.
点评 本题考查了分式的化简求值,正确对分式的分子、分母分解因式,对分式进行通分、约分是关键.

练习册系列答案
相关题目
17.若一次函数y=(2-m)x-4的图象经过点A(x1,y1)和点B(x2,y2),当x1<x2时,y1>y2,则m的取值范围是( )
| A. | m<2 | B. | m>2 | C. | m≤2 | D. | m≥2 |
11.方程组$\left\{\begin{array}{l}{x+3y=7}\\{3x+9y=21}\end{array}\right.$的解的情况是( )
| A. | 无解 | B. | 有一组解 | C. | 有无穷多解 | D. | 不确定 |
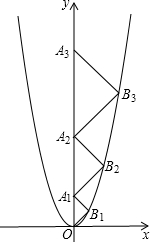 如图,在平面直角坐标系xOy中,点A1,A2,A3,…,An在y轴的正半轴上,点B1,B2,B3,…,Bn在二次函数y=x2位于第一象限的图象上,若△OB1A1,△A1B2A2,△A2B3A3,…,△An-1BnAn都是等腰直角三角形,其中∠B1=∠B2=∠B3=…=∠Bn=90°,则:
如图,在平面直角坐标系xOy中,点A1,A2,A3,…,An在y轴的正半轴上,点B1,B2,B3,…,Bn在二次函数y=x2位于第一象限的图象上,若△OB1A1,△A1B2A2,△A2B3A3,…,△An-1BnAn都是等腰直角三角形,其中∠B1=∠B2=∠B3=…=∠Bn=90°,则: 如图,已知四点A、B、C、D,请用尺规作图完成.(保留画图痕迹)
如图,已知四点A、B、C、D,请用尺规作图完成.(保留画图痕迹)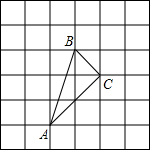 如图,小正方形的边长为1,△ABC的三个顶点都在小正方形的顶点处,判断△ABC的形状,并求出△ABC的面积.
如图,小正方形的边长为1,△ABC的三个顶点都在小正方形的顶点处,判断△ABC的形状,并求出△ABC的面积.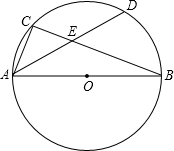 如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=10,AD=8,则AE的长为$\frac{7}{2}$.
如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=10,AD=8,则AE的长为$\frac{7}{2}$.