Question

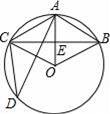
如图，在半径为6cm的⊙O中，点A是劣弧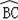的中点，点D是优弧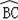上一点，且∠D=30°，下列四个结论：

①OA⊥BC；②BC=6；③sin∠AOB=；④四边形ABOC是菱形．

其中正确结论的序号是（　　）

A．①③ B．①②③④  C．②③④     D．①③④

Answer 1

B【考点】垂径定理；菱形的判定；圆周角定理；解直角三角形．

【专题】几何图形问题．

【分析】分别根据垂径定理、菱形的判定定理、锐角三角函数的定义对各选项进行逐一判断即可．

【解答】解：∵点A是劣弧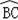的中点，OA过圆心，

∴OA⊥BC，故①正确；

∵∠D=30°，

∴∠ABC=∠D=30°，

∴∠AOB=60°，

∵点A是劣弧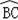的中点，

∴BC=2CE，

∵OA=OB，

∴OA=OB=AB=6cm，

∴BE=AB•cos30°=6×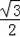=3cm，

∴BC=2BE=6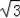cm，故②正确；

∵∠AOB=60°，

∴sin∠AOB=sin60°=，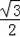

故③正确；

∵∠AOB=60°，

∴AB=OB，

∵点A是劣弧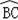的中点，

∴AC=AB，

∴AB=BO=OC=CA，

∴四边形ABOC是菱形，

故④正确．

故选：B．

【点评】本题考查了垂径定理、菱形的判定、圆周角定理、解直角三角形，综合性较强，是一道好题．