题目内容
如图,已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=
 (x>0)经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:
(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:
①双曲线的解析式为y=
 (x>0);②E点的坐标是(5,8);③sin∠COA=
(x>0);②E点的坐标是(5,8);③sin∠COA=
 ;④AC+OB=12
;④AC+OB=12
 .其中正确的结论有( )
.其中正确的结论有( )


A.1个 B.2个 C.3个 D.4个
B【考点】反比例函数综合题.
【分析】过点C作CF⊥x轴于点F,由OB•AC=160可求出菱形的面积,由A点的坐标为(10,0)可求出CF的长,由勾股定理可求出OF的长,故可得出C点坐标,对角线OB、AC相交于D点可求出D点坐标,用待定系数法可求出双曲线y=
 (x>0)的解析式,由反比例函数的解析式与直线BC的解析式联立即可求出E点坐标;由sin∠COA=
(x>0)的解析式,由反比例函数的解析式与直线BC的解析式联立即可求出E点坐标;由sin∠COA=
 可求出∠COA的正弦值;根据A、C两点的坐标可求出AC的长,由OB•AC=160即可求出OB的长.
可求出∠COA的正弦值;根据A、C两点的坐标可求出AC的长,由OB•AC=160即可求出OB的长.
【解答】解:过点C作CF⊥x轴于点F,
∵OB•AC=160,A点的坐标为(10,0),
∴OA•CF=
 OB•AC=
OB•AC=
 ×160=80,菱形OABC的边长为10,
×160=80,菱形OABC的边长为10,
∴CF=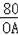
 =
=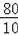
 =8,
=8,
在Rt△OCF中,
∵OC=10,CF=8,
∴OF=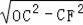
 =
=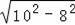
 =6,
=6,
∴C(6,8),
∵点D时线段AC的中点,
∴D点坐标为(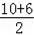
 ,
,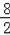
 ),即(8,4),
),即(8,4),
∵双曲线y=
 (x>0)经过D点,
(x>0)经过D点,
∴4=
 ,即k=32,
,即k=32,
∴双曲线的解析式为:y=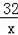
 (x>0),故①错误;
(x>0),故①错误;
∵CF=8,
∴直线CB的解析式为y=8,
∴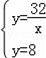
 ,解得x=4,y=8,
,解得x=4,y=8,
∴E点坐标为(4,8),故②错误;
∵CF=8,OC=10,
∴sin∠COA=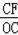
 =
=
 =
=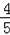
 ,故③正确;
,故③正确;
∵A(10,0),C(6,8),
∴AC=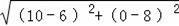
 =4
=4
 ,
,
∵OB•AC=160,
∴OB=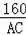
 =
=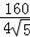
 =8
=8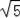
 ,
,
∴AC+OB=4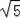
 +8
+8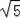
 =12
=12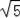
 ,故④正确.
,故④正确.
故选:B.
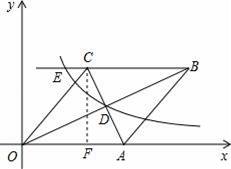

【点评】本题考查的是反比例函数综合题,涉及到菱形的性质及反比例函数的性质、锐角三角函数的定义等相关知识,难度适中.

某校开展了“我最喜爱的老师”评选活动.确定如下评选方案:有学生和教师代表对4名候选教师进行投票,每票选1名候选教师,每位候选教师得到的教师票数的5倍与学生票数的和作为该教师的总票数.以下是根据学生和教师代表投票结果绘制的统计表和条形统计图(不完整).
学生投票结果统计表
| 候选教师 | 丁老师 | 俞老师 | 李老师 | 陈老师 |
| 得票数 | 460 | 200 | 140 | 300 |
(1)若共有25位教师代表参加投票,则李老师得到的教师票数是多少?请补全条形统计图.(画在答案卷相对应的图上)
(2)丁老师与李老师得到的学生总票数是600,且丁老师得到的学生票数是李老师得到的学生票数的3倍多40票,求丁老师与李老师得到的学生票数分别是多少?
(3)在(1)、(2)的条件下,若总得票数较高的2名教师推选到市参评,你认为推选到市里的是两位老师?为什么?


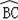
 的中点,点D是优弧
的中点,点D是优弧
 ;③sin∠AOB=
;③sin∠AOB=
 ;④四边形ABOC是菱形.
;④四边形ABOC是菱形.


 ;
;
 =1.414,
=1.414,

