题目内容
嘉淇想证明三角形内角和是180°和其他一些的命题.请完成下列一些命题和证明.
(1)怎样证明三角形内角和是180°呢?
(2)已知命题:等腰三角形底边上的中线和顶角的角平分线重合,证明这个命题,并写出它的逆命题,逆命题成立吗?
命题: 底边上的中线和顶角的角平分线重合的三角形是等腰三角形
证明: 证明:在△ABD和△ACD中,
∵
 ,
,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD
由此我们不难发现: 此命题是互逆命题
那么怎样证明呢?请写出证明过程.(可以画出作图痕迹.)


【考点】命题与定理;等腰三角形的性质.
【分析】(1)先写出已知、证明,过点C作CD∥AB,点E为BC的延长线上一点,利用平行线的性质得到∠1=∠A,∠2=∠B,然后根据平角的定义进行证明;
(2)根据证明的步骤,先写出已知、求证,再写出证明过程,最后写出逆命题即可.
【解答】解:(1)已知:△ABC,如图1,
求证:∠A+∠B+∠C=180°,
证明:过点C作CD∥AB,点E为BC的延长线上一点,如图,
∵CD∥AB,
∴∠1=∠A,∠2=∠B,
∵∠C+∠1+∠2=180°,
∴∠A+∠B+∠C=180°.
(2)如图2,已知:△ABC中,AB=AC,AD是BC边的中线,
求证:∠BAD=∠CAD.
证明:在△ABD和△ACD中,

 ,
,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD.
它的逆命题是:底边上的中线和顶角的角平分线重合的三角形是等腰三角形,成立.




【点评】本题考查了三角形内角和定理:三角形内角和是180°.本题的关键时把三角形三个角的和转化为一个平角,同时注意文字题证明的步骤书写.

某校开展了“我最喜爱的老师”评选活动.确定如下评选方案:有学生和教师代表对4名候选教师进行投票,每票选1名候选教师,每位候选教师得到的教师票数的5倍与学生票数的和作为该教师的总票数.以下是根据学生和教师代表投票结果绘制的统计表和条形统计图(不完整).
学生投票结果统计表
| 候选教师 | 丁老师 | 俞老师 | 李老师 | 陈老师 |
| 得票数 | 460 | 200 | 140 | 300 |
(1)若共有25位教师代表参加投票,则李老师得到的教师票数是多少?请补全条形统计图.(画在答案卷相对应的图上)
(2)丁老师与李老师得到的学生总票数是600,且丁老师得到的学生票数是李老师得到的学生票数的3倍多40票,求丁老师与李老师得到的学生票数分别是多少?
(3)在(1)、(2)的条件下,若总得票数较高的2名教师推选到市参评,你认为推选到市里的是两位老师?为什么?


 的中点,点D是优弧
的中点,点D是优弧
 ;③sin∠AOB=
;③sin∠AOB=
 ;④四边形ABOC是菱形.
;④四边形ABOC是菱形.


 =1.414,
=1.414,





 ,试求y与x的函数关系式.
,试求y与x的函数关系式.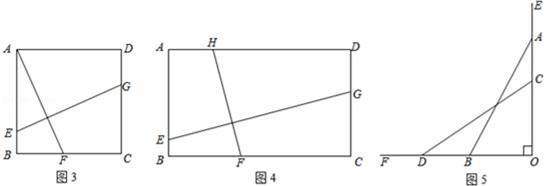


 交x轴于A点,交y轴于B点,点C是线段AB的中点,连接OC,然后将直线OC绕点C逆时针旋转30°交x轴于点D,再过D点作直线DC1∥OC,交AB与点C1,然后过C1点继续作直线D1C1∥OC,交x轴于点D1,并不断重复以上步骤,记△OCD的面积为S1,△DC1D1的面积为S2,依此类推,后面的三角形面积分别是S3,S4…,那么S1=
交x轴于A点,交y轴于B点,点C是线段AB的中点,连接OC,然后将直线OC绕点C逆时针旋转30°交x轴于点D,再过D点作直线DC1∥OC,交AB与点C1,然后过C1点继续作直线D1C1∥OC,交x轴于点D1,并不断重复以上步骤,记△OCD的面积为S1,△DC1D1的面积为S2,依此类推,后面的三角形面积分别是S3,S4…,那么S1= 
 ,若S=S1+S2+S3+…+Sn,当n无限大时,S的值无限接近于 .
,若S=S1+S2+S3+…+Sn,当n无限大时,S的值无限接近于 .







