题目内容
17.解不等式组$\left\{\begin{array}{l}3({x+2})<x+12\\ \frac{x}{2}≥\frac{x-1}{3}\end{array}\right.$,把解集在数轴上表示出来,并写出它的整数解.分析 分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可.
解答 解:$\left\{\begin{array}{l}{3(x+2)<x+12①}\\{\frac{x}{2}≥\frac{x-1}{3}②}\end{array}\right.$,
由①得,x<3,
由②得,x≥-2,
故不等式组的解集为:-2≤x<3,其整数解为:-2,-1,0,1,2.
在数轴上表示为: .
.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
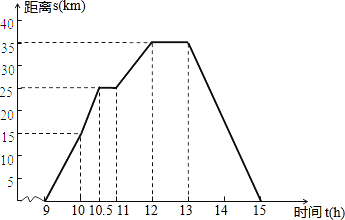 小明在某周末上午9时骑自行车离开家去绿道锻炼,15时回家,已知自行车离家的距离s(km)与时间t(h)之间的关系如图所示.根据图象回答下列问题:
小明在某周末上午9时骑自行车离开家去绿道锻炼,15时回家,已知自行车离家的距离s(km)与时间t(h)之间的关系如图所示.根据图象回答下列问题: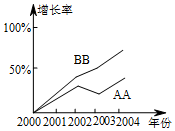 如图,是两种品牌的方便面销售增长率折线统计图,则AA牌方便面2003年的销售量低于2002年的销售量,2002年BB牌方便面的销售量高于AA牌方便面的销售量(填“高于”“低于”“不一定高于”)
如图,是两种品牌的方便面销售增长率折线统计图,则AA牌方便面2003年的销售量低于2002年的销售量,2002年BB牌方便面的销售量高于AA牌方便面的销售量(填“高于”“低于”“不一定高于”) 有理数a,b,c在数轴上的位置如图所示,则化简:|a-b|-|c-a|-|b+c|=-2c.
有理数a,b,c在数轴上的位置如图所示,则化简:|a-b|-|c-a|-|b+c|=-2c.