题目内容
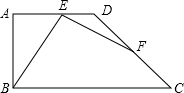 如图,梯形ABCD,AD∥BC,∠ABC=2∠BCD=90°,点E在AD上,点F在DC上,∠BEF=∠A,AB=AD,试猜想EB和EF的数量关系.
如图,梯形ABCD,AD∥BC,∠ABC=2∠BCD=90°,点E在AD上,点F在DC上,∠BEF=∠A,AB=AD,试猜想EB和EF的数量关系.考点:全等三角形的判定与性质,等腰直角三角形,梯形
专题:计算题
分析: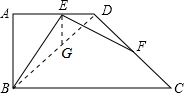 如图,连接BD,则△BCD为等腰直角三角形;作EG⊥AD交BD于点G,则△DEG为等腰直角三角形.证明△BEG≌△FED即可得到EB和EF的数量关系.
如图,连接BD,则△BCD为等腰直角三角形;作EG⊥AD交BD于点G,则△DEG为等腰直角三角形.证明△BEG≌△FED即可得到EB和EF的数量关系.
 如图,连接BD,则△BCD为等腰直角三角形;作EG⊥AD交BD于点G,则△DEG为等腰直角三角形.证明△BEG≌△FED即可得到EB和EF的数量关系.
如图,连接BD,则△BCD为等腰直角三角形;作EG⊥AD交BD于点G,则△DEG为等腰直角三角形.证明△BEG≌△FED即可得到EB和EF的数量关系.解答: 解:EB=EF,理由如下:
解:EB=EF,理由如下:
如图,连接BD,则△BCD为等腰直角三角形;作EG⊥AD交BD于点G,则△DEG为等腰直角三角形.
∴DE=EG,∠DEG=∠BEF=90°,∠EGB=135°,
∴∠BEG=∠FED,
∵∠ABC=2∠BCD=90°,
∴∠C=45°,
∴∠EDC=135°,
在△BEG和△FED中,
,
∴△BEG≌△FED(ASA),
∴EB=EF.
 解:EB=EF,理由如下:
解:EB=EF,理由如下:如图,连接BD,则△BCD为等腰直角三角形;作EG⊥AD交BD于点G,则△DEG为等腰直角三角形.
∴DE=EG,∠DEG=∠BEF=90°,∠EGB=135°,
∴∠BEG=∠FED,
∵∠ABC=2∠BCD=90°,
∴∠C=45°,
∴∠EDC=135°,
在△BEG和△FED中,
|
∴△BEG≌△FED(ASA),
∴EB=EF.
点评:该题目考查了全等三角形的判定和性质、等腰直角三角形的性质,关键是分析出辅助线的作法.

练习册系列答案
相关题目
数轴上与坐标为3的点距离小于7的点的坐标x满足( )
| A、0<x-3<7 |
| B、-7<x-3<7 |
| C、-7≤x-3≤7 |
| D、x-3<7或x-3>7 |
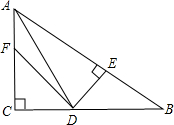 如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;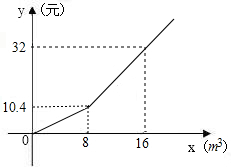 为了节约用水,某城市制定了两种如图用水标准,设某户每月用水量为xm3,应缴水费为y元,请你根据图象回答下列问题:
为了节约用水,某城市制定了两种如图用水标准,设某户每月用水量为xm3,应缴水费为y元,请你根据图象回答下列问题: 已知:如图,AB∥CD,∠B=33°,∠E=12°,则∠D的度数为
已知:如图,AB∥CD,∠B=33°,∠E=12°,则∠D的度数为