题目内容

12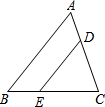．如图所示，△ABC中，点D、E分别是AC、BC边上的点，且DE∥AB，CD：CA﹦2：3，△ABC的面积是18，则△DEC的面积是（　　）
A．8B．9C．12D．15

分析 根据已知条件得到△CDE∽△CAB，根据相似三角形的性质得出$\frac{{S}_{△DEC}}{{S}_{△ABC}}$=（$\frac{CD}{CA}$）2，代入求出即可．

解答 解：∵AD：DC=1：2，
∴CD：CA=2：3，
∵DE∥AB，
∴△CDE∽△CAB，
∴$\frac{{S}_{△DEC}}{{S}_{△ABC}}$=（$\frac{CD}{CA}$）2=（$\frac{2}{3}$）2=$\frac{4}{9}$，
∵△ABC的面积是18，
∴△DEC的面积是8．
故选：A．

点评 本题考查了相似三角形的性质和判定，熟练掌握相似三角形的面积比等于相似比的平方是解题的关键．

练习册系列答案
相关题目
2．计算：
（1）（$\sqrt{3}-\sqrt{5}$）（$\sqrt{3}+\sqrt{5}$）-（$\sqrt{10}-\sqrt{2}$）2
（2）$\sqrt{18}$$\sqrt{\frac{9}{2}}$-$\frac{\sqrt{3}+\sqrt{6}}{\sqrt{3}}$$+（\sqrt{3}-2）^{0}$$+\sqrt{（1-\sqrt{2}）^{2}}$．
3．计算：
（1）（π-3.14）0-|-3|+（$\frac{1}{2}$）-1+（-1）2016
（2）$\frac{x-1}{{x}^{2}-4x+4}$÷$\frac{{x}^{2}-1}{{x}^{2}-4}$．
20．（1）（$\sqrt{48}$-4$\sqrt{\frac{1}{8}}$）-（3$\sqrt{\frac{1}{3}}$-2$\sqrt{0.5}$）
（2）（3$\sqrt{12}$-2$\sqrt{\frac{1}{3}}$+$\sqrt{48}$）÷2$\sqrt{3}$
（3）（7+4$\sqrt{3}$）（7-4$\sqrt{3}$）-（3$\sqrt{5}$-1）2
（4）2$\sqrt{\frac{1}{3}}$×3$\sqrt{2}$+$\sqrt{8}$+|$\sqrt{2}$-1|-π0+（$\frac{1}{2}$）-1．
7．若m＞n，下列不等式不一定成立的是（　　）
A．m+2＞n+2B．2m＞2nC．-2m＜-2nD．m2＞n2
17．先将分式（1+$\frac{3}{x-1}$）÷$\frac{x+2}{{x}^{2}-1}$化简，再选择使原式有意义而你又喜欢的数代入求值．
4．若二次根式$\frac{\sqrt{x+3}}{x}$有意义，则自变量x的取值范围是x≥-3且x≠0．
1．计算或化简：
（1）$\frac{{a}^{2}-{b}^{2}}{{a}^{2}+2ab+{b}^{2}}$
（2）2-$\frac{4}{x+2}$-x．
2．如图，平行四边形ABCD的顶点C在y轴正半轴上，CD平行于x轴，直线AC交x轴于点E，BC⊥AC，连接BE，反比例函数y=$\frac{k}{x}$（x＞0）的图象经过点D，已知S△BCE=2，则k的值是4．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网