题目内容
1．计算或化简：（1）$\frac{{a}^{2}-{b}^{2}}{{a}^{2}+2ab+{b}^{2}}$
（2）2-$\frac{4}{x+2}$-x．
分析 （1）分别根据平方差公式与完全平方公式把分子与分母因式分解，再约分即可；
（2）先通分，再把分子相加减即可．
解答 解：（1）原式=$\frac{（a+b）（a-b）}{（a+b）^{2}}$
=$\frac{a-b}{a+b}$；
（2）原式=$\frac{2（x+2）}{x+2}$-$\frac{4}{x+2}$-$\frac{x（x+2）}{x+2}$
=$\frac{2（x+2）-4-x（x+2）}{x+2}$
=$\frac{2x+4-4-{x}^{2}-2x}{x+2}$
=$\frac{-{x}^{2}}{x+2}$．
点评 本题考查的是分式的加减，熟知异分母分式加减法法则是解答此题的关键．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
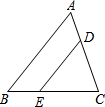如图所示，△ABC中，点D、E分别是AC、BC边上的点，且DE∥AB，CD：CA﹦2：3，△ABC的面积是18，则△DEC的面积是（ ）
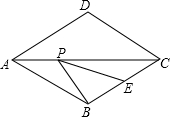如图，菱形ABCD的边长为4，∠DAB=60°，E为BC的中点，在对角线AC上存在一点P，使△PBE的周长最小，则△PBE的周长的最小值为2$\sqrt{3}$+2．
