题目内容
20.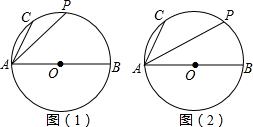 如图,AB是⊙O的直径,C、P是弧AB上两点,AB=25,AC=7.
如图,AB是⊙O的直径,C、P是弧AB上两点,AB=25,AC=7.(1)如图(1),若点P是弧AB的中点,求PA的长;
(2)如图(2),若点P是弧BC的中点,求PA的长.
分析 (1)根据圆周角的定理,∠APB=90°,p是弧AB的中点,所以三角形APB是等腰三角形,利用特殊角的三角函数即可求得;
(2)根据垂径定理得出OP垂直平分BC,得出OP∥AC,从而得出△ACB∽△0NP,根据对应边成比例求得ON、AN的长,利用勾股定理求得NP的长,进而求得PA.
解答 解:(1)如图(1)所示,连接PB,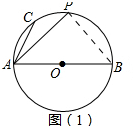
∵AB是⊙O的直径且P是$\widehat{AB}$的中点,
∴∠PAB=∠PBA=45°,∠APB=90°,
又∵在等腰三角形△APB中有AB=25,
∴PA=$\frac{AB}{\sqrt{2}}$=$\frac{25\sqrt{2}}{2}$;
(2)如图(2)所示:连接BC.OP相交于M点,作PN⊥AB于点N,
∵P点为弧BC的中点,
∴OP⊥BC,∠OMB=90°,
又因为AB为直径,
∴∠ACB=90°,
∴∠ACB=∠OMB,
∴OP∥AC,
∴∠CAB=∠POB,
又因为∠ACB=∠ONP=90°,
∴△ACB∽△ONP
∴$\frac{AB}{OP}$=$\frac{AC}{ON}$,
又∵AB=25,AC=7,OP=$\frac{25}{2}$,
代入得 ON=$\frac{7}{2}$,
∴AN=OA+ON=16,
∴在Rt△OPN中,有NP2=OP2-ON2=24
在Rt△ANP中 有PA=$\sqrt{A{N}^{2}+N{P}^{2}}$=$\sqrt{832}$=8$\sqrt{13}$
∴PA=8$\sqrt{13}$.
点评 本题考查了圆周角的定理,垂径定理,勾股定理,等腰三角形判定和性质,相似三角形的判定和性质,作出辅助线是本题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
11.矩形有而平行四边形没有的性质是( )
| A. | 对角相等 | B. | 对边相等 | C. | 邻角互补 | D. | 对角线相等 |
12.下列二次根式中,是最简二次根式的是( )
| A. | $\sqrt{0.5}$ | B. | $\sqrt{\frac{1}{5}}$ | C. | $\sqrt{50}$ | D. | $\sqrt{3{x}^{2}+1}$ |
9.若点(a,b)在第四象限,则点Q(-a,b)所在象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
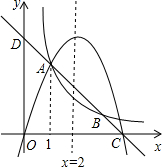 如图,在平面直角坐标系内,二次函数y=ax2+bx(a≠0)、一次函数y=ax+b(a≠0)以及反比例函数y=$\frac{k}{x}({k≠0})$的图象都经过点A,其中一次函数的图象与反比例函数的图象还交于另一点B,且一次函数与x轴、y轴分别交于点C、D.若点A的横坐标为1,该二次函数的对称轴是x=2,则下列结论:①b=-4a;②a+b>k;③8a+4b>k;④a+2b>4k.其中正确结论的个数是( )
如图,在平面直角坐标系内,二次函数y=ax2+bx(a≠0)、一次函数y=ax+b(a≠0)以及反比例函数y=$\frac{k}{x}({k≠0})$的图象都经过点A,其中一次函数的图象与反比例函数的图象还交于另一点B,且一次函数与x轴、y轴分别交于点C、D.若点A的横坐标为1,该二次函数的对称轴是x=2,则下列结论:①b=-4a;②a+b>k;③8a+4b>k;④a+2b>4k.其中正确结论的个数是( )