题目内容
13.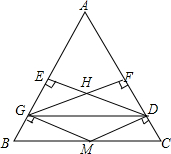 已知:如图,在△ABC中,AB=AC,点M在BC上,BM=CM,作MD⊥AC于D,MG⊥AB于G,GF⊥AC于F,DE⊥AB于E,GF、DE交于点H.求证:四边形MDHG为菱形.
已知:如图,在△ABC中,AB=AC,点M在BC上,BM=CM,作MD⊥AC于D,MG⊥AB于G,GF⊥AC于F,DE⊥AB于E,GF、DE交于点H.求证:四边形MDHG为菱形.
分析 先证明四边形MDHG是平行四边形,再由AAS证明△BGM≡△CDM,得出对应边相等GM=DM,即可得出四边形MDHG为菱形.
解答 证明:∵AB=AC,
∴∠B=∠C,
∵MD⊥AC,MG⊥AB,GF⊥AC,DE⊥AB,
∴MD∥GF,MG∥DE,∠BGM=∠CDM=90°,
∴四边形MDHG是平行四边形,
在△BGM和△CDM中,$\left\{\begin{array}{l}{∠B=∠C}&{\;}\\{∠BGM=∠CDG}&{\;}\\{BM=CM}&{\;}\end{array}\right.$,
∴△BGM≡△CDM(AAS),
∴GM=DM,
∴四边形MDHG为菱形.
点评 本题考查了等腰三角形的性质、平行四边形的判定、全等三角形的判定与性质、菱形的判定;熟练掌握等腰三角形的性质和菱形的判定方法,并能进行推理论证是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

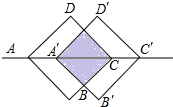 如图所示.正方形ABCD的对角线长为6cm,将此正方形沿对角线AC的方向向右平移2cm得到正方形A′B′C′D′,则平移前后两个图形的重叠部分(阴影部分)的面积为8.
如图所示.正方形ABCD的对角线长为6cm,将此正方形沿对角线AC的方向向右平移2cm得到正方形A′B′C′D′,则平移前后两个图形的重叠部分(阴影部分)的面积为8.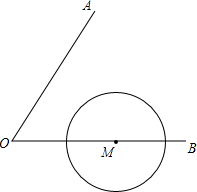 如图,∠AOB=60°,M为OB上的一点,OM=5,若以M为圆心,2.5为半径画⊙M,请通过计算说明OA不和⊙M相切.
如图,∠AOB=60°,M为OB上的一点,OM=5,若以M为圆心,2.5为半径画⊙M,请通过计算说明OA不和⊙M相切. 如图,BD平分∠ABC,∠BAD+∠BCD=180°,求证:AD=CD.
如图,BD平分∠ABC,∠BAD+∠BCD=180°,求证:AD=CD.