题目内容
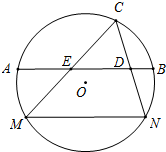 如图所示,MN是圆O中一条固定的弦,劣弧MN的度数为120°,点C是圆O上一个动点(不与M、N重合).连接MC、NC,D、E分别是NC和MC的中点,直线DE交圆O于点A、B.已知圆O的半径为
如图所示,MN是圆O中一条固定的弦,劣弧MN的度数为120°,点C是圆O上一个动点(不与M、N重合).连接MC、NC,D、E分别是NC和MC的中点,直线DE交圆O于点A、B.已知圆O的半径为| 3 |
考点:三角形中位线定理,勾股定理,圆心角、弧、弦的关系
专题:动点型
分析:判断出点C在劣弧MN上且点C在劣弧MN的中点时,AB的长度最小,根据三角形的中位线平行于第三边并且等于第三边的一半可得DE=
MN,从而得到此时AE+BD的值最小,连接OA、OM、连接OC与MN、AB分别相交于点F、G,然后求出OF、MF,再求出OG,然后利用勾股定理列式求出AG,再根据AE+BD=2AG-DE计算即可得解.
| 1 |
| 2 |
解答: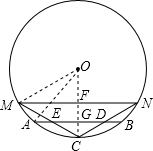 解:∵D、E分别是NC和MC的中点,
解:∵D、E分别是NC和MC的中点,
∴点C在劣弧MN上且点C在劣弧MN的中点时,AB的长度最小,
此时DE=
MN,
连接OA、OM、连接OC与MN、AB分别相交于点F、G,
∵劣弧MN的度数为120°,
∴∠OMN=
(180°-120°)=30°,
∵圆O的半径为
,
∴OF=
×
=
,
MF=
×
=
,
∵D、E分别是NC和MC的中点,
∴FG=
(OC-OF)=
(
-
)=
,
∴OG=OF+FG=
+
=
,
在Rt△AOG中,AG=
=
=
,
∴AE+BD=2AG-DE=2×
-
=
.
故答案为:
.
 解:∵D、E分别是NC和MC的中点,
解:∵D、E分别是NC和MC的中点,∴点C在劣弧MN上且点C在劣弧MN的中点时,AB的长度最小,
此时DE=
| 1 |
| 2 |
连接OA、OM、连接OC与MN、AB分别相交于点F、G,
∵劣弧MN的度数为120°,
∴∠OMN=
| 1 |
| 2 |
∵圆O的半径为
| 3 |
∴OF=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
MF=
| ||
| 2 |
| 3 |
| 3 |
| 2 |
∵D、E分别是NC和MC的中点,
∴FG=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 4 |
∴OG=OF+FG=
| ||
| 2 |
| ||
| 4 |
3
| ||
| 4 |
在Rt△AOG中,AG=
| AO2-OG2 |
(
|
| ||
| 4 |
∴AE+BD=2AG-DE=2×
| ||
| 4 |
| 3 |
| 2 |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,勾股定理,圆心角、弧、弦的关系,难点在于判断出点C在在劣弧MN的中点时AE+BD的值最小.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
式子:-x+1,x+3,
,S=
ab中,整式的个数是( )
| x |
| x+y |
| 1 |
| 2 |
| A、4 | B、3 | C、2 | D、1 |
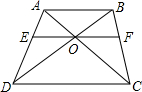 如图所示,在梯形ABCD中,AB∥CD,AB=5,CD=10,AC与BD交于点O,过O作EF∥AB,交AD于E,交BC于F,求EO的长.
如图所示,在梯形ABCD中,AB∥CD,AB=5,CD=10,AC与BD交于点O,过O作EF∥AB,交AD于E,交BC于F,求EO的长. 如图,某船向正东航行,在A处望见海岛C在北偏东60°,前进6海里到B点,测得海岛C在北偏东45°,已知在该岛周围6海里内有暗礁,问船继续向正东航行,有触礁的危险吗?
如图,某船向正东航行,在A处望见海岛C在北偏东60°,前进6海里到B点,测得海岛C在北偏东45°,已知在该岛周围6海里内有暗礁,问船继续向正东航行,有触礁的危险吗?