题目内容
二次函数与x轴交于(0,0),(12,0),且顶点到x轴的距离为3,求函数解析式.
考点:待定系数法求二次函数解析式
专题:
分析:根据条件可求得顶点坐标为(6,3)或(6,-3),可设为顶点式,再把(0,0)代入可求出函数解析式.
解答:解:∵(0,0),(12,0),且顶点到x轴的距离为3,
∴顶点坐标为(6,3)或(6,-3),
当顶点坐标为(6,3)时,
设二次函数解析式为y=a(x-6)2+3,
又过点(0,0),代入可求得a=-
,
∴y=-
(x-6)2+3,即y=-
x2+x;
当顶点坐标为(6,-3)时,
设二次函数解析式为y=a(x-6)2-3,
又过点(0,0),代入可求得a=
,
∴y=
(x-6)2-3,即y=
x2-x;
综上可知y=-
x2+x或y=
x2-x.
∴顶点坐标为(6,3)或(6,-3),
当顶点坐标为(6,3)时,
设二次函数解析式为y=a(x-6)2+3,
又过点(0,0),代入可求得a=-
| 1 |
| 12 |
∴y=-
| 1 |
| 12 |
| 1 |
| 12 |
当顶点坐标为(6,-3)时,
设二次函数解析式为y=a(x-6)2-3,
又过点(0,0),代入可求得a=
| 1 |
| 12 |
∴y=
| 1 |
| 12 |
| 1 |
| 12 |
综上可知y=-
| 1 |
| 12 |
| 1 |
| 12 |
点评:本题主要考查待定系数法求函数解析式,根据题意得出顶点坐标是解题的关键,注意分类讨论思想的应用.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
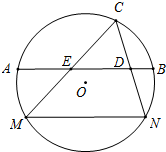 如图所示,MN是圆O中一条固定的弦,劣弧MN的度数为120°,点C是圆O上一个动点(不与M、N重合).连接MC、NC,D、E分别是NC和MC的中点,直线DE交圆O于点A、B.已知圆O的半径为
如图所示,MN是圆O中一条固定的弦,劣弧MN的度数为120°,点C是圆O上一个动点(不与M、N重合).连接MC、NC,D、E分别是NC和MC的中点,直线DE交圆O于点A、B.已知圆O的半径为 如图所示,已知△ADE∽△ABC,且AD=3,BD=CE=4,求AC的长.
如图所示,已知△ADE∽△ABC,且AD=3,BD=CE=4,求AC的长.