题目内容
 如图,某船向正东航行,在A处望见海岛C在北偏东60°,前进6海里到B点,测得海岛C在北偏东45°,已知在该岛周围6海里内有暗礁,问船继续向正东航行,有触礁的危险吗?
如图,某船向正东航行,在A处望见海岛C在北偏东60°,前进6海里到B点,测得海岛C在北偏东45°,已知在该岛周围6海里内有暗礁,问船继续向正东航行,有触礁的危险吗?考点:解直角三角形的应用-方向角问题
专题:
分析:判断有无危险只要求出点C到AB的距离,与6海里比较大小就可以.
解答: 解:过点C作CD⊥AB于点D,
解:过点C作CD⊥AB于点D,
∵∠CAD=90°-60°=30°,∠CBD=90°-45°=45°,
∴BD=CD,
设CD=x,
∴AD=AB+6=6+x,
在Rt△CAD中,tan∠CAD=
,
∴
=
,
3x=6
+
x,
(3-
)x=6
,
解得x=
=3
+3>6,
答:若船继续向东航行,无触礁危险.
 解:过点C作CD⊥AB于点D,
解:过点C作CD⊥AB于点D,∵∠CAD=90°-60°=30°,∠CBD=90°-45°=45°,
∴BD=CD,
设CD=x,
∴AD=AB+6=6+x,
在Rt△CAD中,tan∠CAD=
| CD |
| AD |
∴
| ||
| 3 |
| x |
| x+6 |
3x=6
| 3 |
| 3 |
(3-
| 3 |
| 3 |
解得x=
6
| ||
3-
|
| 3 |
答:若船继续向东航行,无触礁危险.
点评:本题考查了解直角三角形的应用,解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
已知M(a,3)和N(4,b)关于y轴对称,则(a+b)2000的值为( )
| A、1 |
| B、-1 |
| C、72000 |
| D、-72000 |
 已知,如图,点C为线段AB上一点,AC=
已知,如图,点C为线段AB上一点,AC=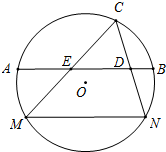 如图所示,MN是圆O中一条固定的弦,劣弧MN的度数为120°,点C是圆O上一个动点(不与M、N重合).连接MC、NC,D、E分别是NC和MC的中点,直线DE交圆O于点A、B.已知圆O的半径为
如图所示,MN是圆O中一条固定的弦,劣弧MN的度数为120°,点C是圆O上一个动点(不与M、N重合).连接MC、NC,D、E分别是NC和MC的中点,直线DE交圆O于点A、B.已知圆O的半径为 如图,正方形网格中每个小正方形的边长为1.
如图,正方形网格中每个小正方形的边长为1. 如图所示,已知△ADE∽△ABC,且AD=3,BD=CE=4,求AC的长.
如图所示,已知△ADE∽△ABC,且AD=3,BD=CE=4,求AC的长.