题目内容
7.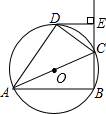 如图.四边形ABCD内接于⊙O,AC是⊙O的直径,DE⊥BC于E,CD平分∠ACE.
如图.四边形ABCD内接于⊙O,AC是⊙O的直径,DE⊥BC于E,CD平分∠ACE.(1)求证:DE是⊙O的切线.
(2)若∠ACB=60°,CE=1,求直径AC的长.
分析 (1)连接OD,根据角之间的互余关系可得∠ODE=∠DEC=90°,故DE⊥OD,即DE是⊙O的切线;
(2)根据圆周角定理,可得在Rt△CED中,∠CED=90°,∠EDC=30°,有CD=2CE;在Rt△ACD中,∠ADC=90°,∠CAD=30°,有AC=2CD=4CE,即可得出答案.
解答  (1)证明:连接OD,
(1)证明:连接OD,
∵CD平分∠ACE,
∴∠DCA=∠ECD.
∵OC=OD,
∴∠OCD=∠ODC,
∴∠ODC=∠ECD,
∴OD∥BE.
∵DE⊥BE,
∴DE⊥OD.
∴DE是⊙O的切线;
(2)解:∵AC是直径,
∴∠ABC=∠ADC=90°.
∵∠BCA=60°,
∴∠BAC=30°,
∴∠ACE=120°.
∵CD平分∠ACE,
∴∠ACD=∠ECD=60°.
∴∠CAD=∠EDC=30°.
∵在Rt△CED中,∠CED=90°,∠EDC=30°,
∴CD=2CE.
∵在Rt△ACD中,∠ADC=90°,∠CAD=30°,
∴AC=2CD=4CE.
∵CE的长是1cm,
∴AC的长是4cm.
点评 本题考查常见的几何题型,包括切线的判定,及线段长度的求法,要求学生掌握常见的解题方法,并能结合图形选择简单的方法解题.

练习册系列答案
相关题目
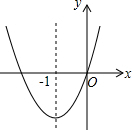 如图,已知经过原点的抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=-1,下列结论中:?①ab>0,?②a+b+c>0,?③当-2<x<0时,y<0,④2a-b=0,正确的个数是( )
如图,已知经过原点的抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=-1,下列结论中:?①ab>0,?②a+b+c>0,?③当-2<x<0时,y<0,④2a-b=0,正确的个数是( )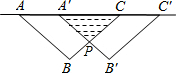 如图,把等腰Rt△ABC沿AC方向平移到等腰Rt△A′B′C′的位置时,它们重叠的部分的面积是Rt△ABC面积的$\frac{1}{4}$.若AB=$\sqrt{2}$cm,则它移动的距离AA′=1cm.
如图,把等腰Rt△ABC沿AC方向平移到等腰Rt△A′B′C′的位置时,它们重叠的部分的面积是Rt△ABC面积的$\frac{1}{4}$.若AB=$\sqrt{2}$cm,则它移动的距离AA′=1cm. 如图,在△ABC中,∠ACB=90°,BC=AC=1,将△ABC绕点A顺时针旋转90°后得到△ADE,则BC边扫过部分图形(即阴影部分)的面积为$\frac{1}{4}$π(结果保留π).
如图,在△ABC中,∠ACB=90°,BC=AC=1,将△ABC绕点A顺时针旋转90°后得到△ADE,则BC边扫过部分图形(即阴影部分)的面积为$\frac{1}{4}$π(结果保留π).