题目内容
15.已知二次函数y=ax2+bx-$\frac{3}{2}$的图象与y轴交于点B.(1)若二次函数的图象经过点A(1,1),
①二次函数的对称轴为直线x=1,求此二次函数的解析式;
②对于任意的正数a,当x>n时,y随x的增大而增大,请求出n的取值范围.
(2)若二次函数的图象的对称轴为直线x=-1,且直线y=2x-2与直线l也关于直线x=-1对称,且二次函数的图象在-5<x<-4这一段位于直线l的上方,在1<x<2这一段位于直线y=2x-2的下方,求此二次函数的解析式.
分析 (1)①由题意得出$\left\{\begin{array}{l}{a+b-\frac{3}{2}=1}\\{-\frac{b}{2a}=1}\end{array}\right.$,求得$\left\{\begin{array}{l}{a=-\frac{5}{2}}\\{b=5}\end{array}\right.$,从而求得二次函数的解析式;
②由二次函数的图象经过点A(1,1),得出a+b$\frac{3}{2}$=1,进而得出b=$\frac{5}{2}$-a,根据题意对称轴x=n=-$\frac{\frac{5}{2}-a}{2a}$=-$\frac{5}{4a}$+$\frac{1}{2}$,由a>0,则-$\frac{5}{4a}$<0,即可求得n<$\frac{1}{2}$;
(2)由题意得出抛物线经过(-4,2),代入解析式得出16a-4b-$\frac{3}{2}$=0,根据对称轴x=-1,得出b=2a,代入即可求得a、b的值.
解答 解:(1)①由题意得$\left\{\begin{array}{l}{a+b-\frac{3}{2}=1}\\{-\frac{b}{2a}=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{5}{2}}\\{b=5}\end{array}\right.$.
∴此二次函数的解析式为y=-$\frac{5}{2}$x2+5x-$\frac{3}{2}$;
②∵二次函数的图象经过点A(1,1),
∴a+b$\frac{3}{2}$=1,
∴b=$\frac{5}{2}$-a,
∵当x>n时,y随x的增大而增大,
∴对称轴x=n=-$\frac{b}{2a}$=-$\frac{\frac{5}{2}-a}{2a}$=-$\frac{5}{4a}$+$\frac{1}{2}$,
∵a>0,∴-$\frac{5}{4a}$<0,
∴n≥$\frac{1}{2}$;
(2)由直线y=2x-2可知:直线y=2x-2与直线x=-1的交点为(-1,-4),与x轴的交点为(1,0),
∵直线y=2x-2与直线l也关于直线x=-1对称,
∴直线l与x轴的交点为(-3,0),
∴直线l为:y=-2x-6
由题意:抛物线经过(-4,2),
∴16a-4b-$\frac{3}{2}$=2,
∵对称轴x=-$\frac{b}{2a}$=-1,
∴$\left\{\begin{array}{l}{a=\frac{7}{16}}\\{b=\frac{7}{8}}\end{array}\right.$,
∴此二次函数的解析式为y=$\frac{7}{16}$x2+$\frac{7}{8}$x-$\frac{3}{2}$.
点评 本题考查了二次函数的性质以及待定系数法求二次函数的解析式,根据题意列出方程组是解题的关键.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | -3.5 | -1 | 0.5 | 1 | 0.5 | -1 | -3.5 | … |
①函数有最大值,且最大值为1;
②若x0满足y=ax02+bx+c,则2<x0<3或-1<x0<0;
③若方程ax2+bx+c+m=0有两个不等的实数根且m<-1;
④对于任意实数m,当m≠1时,有m(am+b)<$\frac{1}{2}$.
其中正确结论的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 如图,△ABC的三边长为AC=5,BC=6,AB=7,⊙O与△ABC的三边相切于D,E,F.
如图,△ABC的三边长为AC=5,BC=6,AB=7,⊙O与△ABC的三边相切于D,E,F.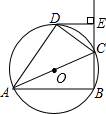 如图.四边形ABCD内接于⊙O,AC是⊙O的直径,DE⊥BC于E,CD平分∠ACE.
如图.四边形ABCD内接于⊙O,AC是⊙O的直径,DE⊥BC于E,CD平分∠ACE. 如图所示.∠AOB=90°,ON是∠AOC的平分线,OM是∠BOC的平分线,求∠MON的大小.
如图所示.∠AOB=90°,ON是∠AOC的平分线,OM是∠BOC的平分线,求∠MON的大小.