题目内容
4.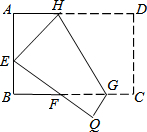 如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是8cm.
如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是8cm.
分析 设AH=a,则DH=AD-AH=8-a,通过勾股定理即可求出a值,再根据同角的余角互补可得出∠BFE=∠AEH,从而得出△EBF∽△HAE,根据相似三角形的周长比等于对应比即可求出结论.
解答 解:设AH=a,则DH=AD-AH=8-a,
在Rt△AEH中,∠EAH=90°,AE=4,AH=a,EH=DH=8-a,
∴EH2=AE2+AH2,即(8-a)2=42+a2,
解得:a=3.
∵∠BFE+∠BEF=90°,∠BEF+∠AEH=90°,
∴∠BFE=∠AEH.
又∵∠EAH=∠FBE=90°,
∴△EBF∽△HAE,
∴$\frac{{C}_{△EBF}}{{C}_{△HAE}}$=$\frac{BE}{AH}$=$\frac{AB-AE}{AH}$=$\frac{2}{3}$.
∵C△HAE=AE+EH+AH=AE+AD=12,
∴C△EBF=$\frac{2}{3}$C△HAE=8.
故答案为:8.
点评 本题考查了翻折变换、矩形的性质、勾股定理以及相似三角形的判定及性质,解题的关键是找出△EBF∽△HAE.本题属于中档题,难度不大,解决该题型题目时,通过勾股定理求出三角形的边长,再根据相似三角形的性质找出周长间的比例是关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
12.“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场.顺风车行经营的A型车去年6月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的A型车数量相同,则今年6月份A型车销售总额将比去年6月份销售总额增加25%.
(1)求今年6月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A、B两种型号车的进货和销售价格如表:
(1)求今年6月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A、B两种型号车的进货和销售价格如表:
| A型车 | B型车 | |
| 进货价格(元/辆) | 1100 | 1400 |
| 销售价格(元/辆) | 今年的销售价格 | 2400 |
7.已知方程x-2y+3=8,则整式x-2y的值为( )
| A. | 5 | B. | 10 | C. | 12 | D. | 15 |
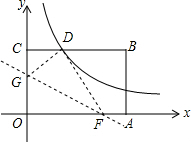 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,AB=BD,反比例函数$y=\frac{k}{x}(k≠0)$在第一象限内的图象经过点D(m,2)和AB边上的点$E(n,\frac{2}{3})$.
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,AB=BD,反比例函数$y=\frac{k}{x}(k≠0)$在第一象限内的图象经过点D(m,2)和AB边上的点$E(n,\frac{2}{3})$.