题目内容
17.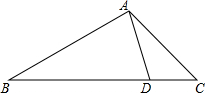 如图,D是△ABC的边BC上一点,AB=8,AD=4,∠DAC=∠B.如果△ABD的面积为15,那么△ACD的面积为( )
如图,D是△ABC的边BC上一点,AB=8,AD=4,∠DAC=∠B.如果△ABD的面积为15,那么△ACD的面积为( )| A. | 15 | B. | 10 | C. | $\frac{15}{2}$ | D. | 5 |
分析 首先证明△ACD∽△BCA,由相似三角形的性质可得:△ACD的面积:△ABC的面积为1:4,因为△ABD的面积为9,进而求出△ACD的面积.
解答 解:∵∠DAC=∠B,∠C=∠C,
∴△ACD∽△BCA,
∵AB=8,AD=4,
∴△ACD的面积:△ABC的面积=($\frac{AD}{AB}$)2=1:4,
∴△ACD的面积:△ABD的面积=1:3,
∵△ABD的面积为15,
∴△ACD的面积=5.
故选D.
点评 本题考查了相似三角形的判定和性质:相似三角形的面积比等于相似比的平方,是中考常见题型.

练习册系列答案
相关题目
7. 下面所给几何体的俯视图是( )
下面所给几何体的俯视图是( )
 下面所给几何体的俯视图是( )
下面所给几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
12.“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场.顺风车行经营的A型车去年6月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的A型车数量相同,则今年6月份A型车销售总额将比去年6月份销售总额增加25%.
(1)求今年6月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A、B两种型号车的进货和销售价格如表:
(1)求今年6月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A、B两种型号车的进货和销售价格如表:
| A型车 | B型车 | |
| 进货价格(元/辆) | 1100 | 1400 |
| 销售价格(元/辆) | 今年的销售价格 | 2400 |
2.在校田径运动会上,小明和其他三名选手参加100米预赛,赛场共设1,2,3,4四条跑道,选手以随机抽签的方式决定各自的跑道.若小明首先抽签,则小明抽到1号跑道的概率是( )
| A. | $\frac{1}{16}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
20.在反比例函数y=$\frac{1-3k}{x}$的图象上有两点A(x1,y1),B(x2,y2),当0<x1<x2时,有y1>y2,则k的取值范围是( )
| A. | k$>\frac{1}{3}$ | B. | k$<\frac{1}{3}$ | C. | k$≥\frac{1}{3}$ | D. | k$≤\frac{1}{3}$ |
 如图,在平面直角坐标系中,已知抛物线y=ax2+bx-2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,-1),该抛物线与BE交于另一点F,连接BC.
如图,在平面直角坐标系中,已知抛物线y=ax2+bx-2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,-1),该抛物线与BE交于另一点F,连接BC.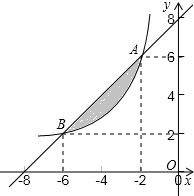 如图A、B两点在函数y=$\frac{k}{x}$(x<0)的图象上.
如图A、B两点在函数y=$\frac{k}{x}$(x<0)的图象上.