题目内容
12.某校数学课题学习小组在“测量教学楼高度”的活动中,设计了以下两种方案:| 课题 | 测量教学楼高度 | |
| 方案 | 方案一 | 方案二 |
| 测量示意图 | 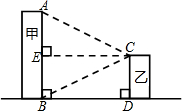 |  |
| 测得数据 | BD=32m,∠ACE=∠BCE=31° | BD=32m,∠DAF=50°,∠CAF=31° |
| 参考数据 | tan31°≈0.60,sin31°≈0.52 cos31°≈0.86 | tan31°≈0.60,tan50°≈1.20, sin50°≈0.77 |
分析 方案一:首先四边形BDCE是矩形,则可得CE=BD=32cm,CD=BE,然后分别在Rt△ACE与Rt△BCE中,利用三角函数的知识,求得AE与BE的长,继而求得答案;
方案二:首先连接AD,易得四边形BDCE是矩形,则可得CE=BD=32cm,CD=BE,然后分别在Rt△ACE与Rt△ABD中,利用三角函数的知识,求得AE与BE的长,继而求得答案
解答 解:方案一:根据题意得:四边形BDCE是矩形,
∴CE=BD=32cm,CD=BE,
在Rt△ACE中,AE=EC•tan31°≈32×0.60=19.20(m),
在Rt△BCE中,BE=EC•tan31°≈32×0.60=19.20(m),
∴AB=AE+BE=38.40m,CD=BE=19.20m;
答:甲教学楼AB的高度为:38.40m;乙教学楼CD的高度为19.20m;
方案二:如图,连接AD,
根据题意得:四边形BDCE是矩形,
∴CE=BD=32cm,CD=BE,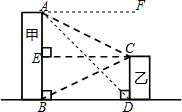
∵在Rt△ACE中,∠ACE=∠CAF=31°,
∴AE=EC•tan31°≈32×0.60=19.20(m),
∵在Rt△ABD中,∠ADB=∠DAF=50°,
∴AB=BD•tan50°≈32×1.20=38.40(m),
∴CD=BE=AB-AE=19.20m.
答:甲教学楼AB的高度为:38.40m;乙教学楼CD的高度为19.20m.
点评 本题考查仰角与俯角的定义.注意能借助仰角与俯角构造直角三角形并解直角三角形是关键.

练习册系列答案
相关题目
3. 如图,AB是⊙O的直径,∠ABC=30°,OA=6,则扇形AOC面积为( )
如图,AB是⊙O的直径,∠ABC=30°,OA=6,则扇形AOC面积为( )
 如图,AB是⊙O的直径,∠ABC=30°,OA=6,则扇形AOC面积为( )
如图,AB是⊙O的直径,∠ABC=30°,OA=6,则扇形AOC面积为( )| A. | 2π | B. | 4π | C. | 6π | D. | 8π |
20. 如图,小“鱼”与大“鱼”是位似图形,已知小“鱼”上一个“顶点”的坐标为(a,b),那么大“鱼”上对应“顶点”的坐标为( )
如图,小“鱼”与大“鱼”是位似图形,已知小“鱼”上一个“顶点”的坐标为(a,b),那么大“鱼”上对应“顶点”的坐标为( )
 如图,小“鱼”与大“鱼”是位似图形,已知小“鱼”上一个“顶点”的坐标为(a,b),那么大“鱼”上对应“顶点”的坐标为( )
如图,小“鱼”与大“鱼”是位似图形,已知小“鱼”上一个“顶点”的坐标为(a,b),那么大“鱼”上对应“顶点”的坐标为( )| A. | (-a,-2b) | B. | (-2a,-b) | C. | (-2a,-2b) | D. | (-b,-2a) |
7.在平面直角坐标系中,经过二、三、四象限的直线l过点(-2,-3).点(-1,a),(0,b),(c,1)都在直线l上,则下列判断正确的是( )
| A. | a<b | B. | c>-1 | C. | a>-3 | D. | c<-2 |
17.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表:
下列结论:(1)ac<0;(2)当x>1时,y的值随x值的增大而减小.(3)3是方程ax2+(b-1)x+c=0的一个根;(4)当-1<x<3时,ax2+(b-1)x+c>0.其中正确的个数为( )
| x | … | -1 | 0 | 1 | 3 | … |
| y | … | -1 | 3 | 5 | 3 | … |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.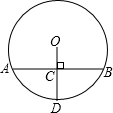 如图,已知⊙O的半径OD与弦AB互相垂直,垂足为点C,若AB=16cm,CD=6cm,则⊙O的半径为( )
如图,已知⊙O的半径OD与弦AB互相垂直,垂足为点C,若AB=16cm,CD=6cm,则⊙O的半径为( )
 如图,已知⊙O的半径OD与弦AB互相垂直,垂足为点C,若AB=16cm,CD=6cm,则⊙O的半径为( )
如图,已知⊙O的半径OD与弦AB互相垂直,垂足为点C,若AB=16cm,CD=6cm,则⊙O的半径为( )| A. | $\frac{25}{3}$cm | B. | 10cm | C. | 8cm | D. | $\frac{19}{3}$cm |
1.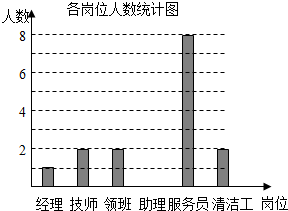 某公司共20名员工,员工基本工资的平均数为2200元.现就其各岗位每人的基本工资情况和各岗位人数,绘制了下列尚不完整的统计图表:各岗位每人的基本工资情况统计表
某公司共20名员工,员工基本工资的平均数为2200元.现就其各岗位每人的基本工资情况和各岗位人数,绘制了下列尚不完整的统计图表:各岗位每人的基本工资情况统计表
请回答下列问题:
(1)将各岗位人数统计图补充完整;
(2)求该公司服务员每人的基本工资;
(3)该公司所有员工基本工资的中位数是1500元,众数是1400元;你认为用基本工资的平均数和中位数来代表该公司员工基本工资的一般水平,哪一个更恰当?请说明理由.
(4)该公司一名员工向经理辞职了,若其他员工的基本工资不变,那么基本工资的平均数就降低了.你认为辞职的可能是哪个岗位上的员工呢?说明理由.
 某公司共20名员工,员工基本工资的平均数为2200元.现就其各岗位每人的基本工资情况和各岗位人数,绘制了下列尚不完整的统计图表:各岗位每人的基本工资情况统计表
某公司共20名员工,员工基本工资的平均数为2200元.现就其各岗位每人的基本工资情况和各岗位人数,绘制了下列尚不完整的统计图表:各岗位每人的基本工资情况统计表| 岗位 | 经理 | 技师 | 领班 | 助理 | 服务员 | 清洁工 |
| 基本工资 | 10000 | 4000 | 2400 | 1600 | 1000 |
(1)将各岗位人数统计图补充完整;
(2)求该公司服务员每人的基本工资;
(3)该公司所有员工基本工资的中位数是1500元,众数是1400元;你认为用基本工资的平均数和中位数来代表该公司员工基本工资的一般水平,哪一个更恰当?请说明理由.
(4)该公司一名员工向经理辞职了,若其他员工的基本工资不变,那么基本工资的平均数就降低了.你认为辞职的可能是哪个岗位上的员工呢?说明理由.
2.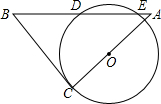 如图,将一块等腰Rt△ABC的直角顶点C放在⊙O上,绕点C旋转三角形,使边AC经过圆心O,某一时刻,斜边AB在⊙O上截得的线段DE=2cm,且BC=7cm,则OC的长为( )
如图,将一块等腰Rt△ABC的直角顶点C放在⊙O上,绕点C旋转三角形,使边AC经过圆心O,某一时刻,斜边AB在⊙O上截得的线段DE=2cm,且BC=7cm,则OC的长为( )
 如图,将一块等腰Rt△ABC的直角顶点C放在⊙O上,绕点C旋转三角形,使边AC经过圆心O,某一时刻,斜边AB在⊙O上截得的线段DE=2cm,且BC=7cm,则OC的长为( )
如图,将一块等腰Rt△ABC的直角顶点C放在⊙O上,绕点C旋转三角形,使边AC经过圆心O,某一时刻,斜边AB在⊙O上截得的线段DE=2cm,且BC=7cm,则OC的长为( )| A. | 3cm | B. | $\frac{20}{7}$cm | C. | $\sqrt{10}$cm | D. | 2$\sqrt{2}$cm |