题目内容
13. 如图,平面直角坐标系中,已知点A(8,0)和点B(0,6),点C是AB的中点,点P在折线AOB上,直线CP截△AOB,所得的三角形与△AOB相似,那么点P的坐标是(0,3)、(4,0)、($\frac{7}{4}$,0).
如图,平面直角坐标系中,已知点A(8,0)和点B(0,6),点C是AB的中点,点P在折线AOB上,直线CP截△AOB,所得的三角形与△AOB相似,那么点P的坐标是(0,3)、(4,0)、($\frac{7}{4}$,0).
分析 分类讨论:当PC∥OA时,△BPC∽△BOA,易得P点坐标为(0,3);当PC∥OB时,△ACP∽△ABO,易得P点坐标为(4,0);当PC⊥AB时,如图,由于∠CAP=∠OAB,则Rt△APC∽Rt△ABC,计算出AB、AC,则可利用比例式计算出AP,于是可得到OP的长,从而得到P点坐标.
解答  解:当PC∥OA时,△BPC∽△BOA,
解:当PC∥OA时,△BPC∽△BOA,
由点C是AB的中点,可得P为OB的中点,
此时P点坐标为(0,3);
当PC∥OB时,△ACP∽△ABO,
由点C是AB的中点,可得P为OA的中点,
此时P点坐标为(4,0);
当PC⊥AB时,如图,
∵∠CAP=∠OAB,
∴Rt△APC∽Rt△ABC,
∴$\frac{AC}{OA}$=$\frac{AP}{AB}$,
∵点A(8,0)和点B(0,6),
∴AB=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵点C是AB的中点,
∴AC=5,
∴$\frac{5}{8}$=$\frac{AP}{10}$,
∴AP=$\frac{25}{4}$,
∴OP=OA-AP=8-$\frac{25}{4}$=$\frac{7}{4}$,
此时P点坐标为($\frac{7}{4}$,0),
综上所述,满足条件的P点坐标为(0,3)、(4,0)、($\frac{7}{4}$,0).
故答案为:(0,3)、(4,0)、($\frac{7}{4}$,0)
点评 本题考查了相似三角形的判定:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;有两组角对应相等的两个三角形相似.也考查了坐标与图形性质.注意分类讨论思想解决此题.

练习册系列答案
相关题目
8.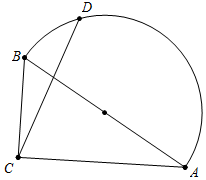 如图,在Rt△ABC中,∠ACB=90°,tan∠CAB=$\frac{\sqrt{3}}{3}$,AB=3,点D在以斜边AB为直径的半圆上,点M是CD的三等分点,当点D沿着半圆,从点A运动到点B时,点M运动的路径长为( )
如图,在Rt△ABC中,∠ACB=90°,tan∠CAB=$\frac{\sqrt{3}}{3}$,AB=3,点D在以斜边AB为直径的半圆上,点M是CD的三等分点,当点D沿着半圆,从点A运动到点B时,点M运动的路径长为( )
 如图,在Rt△ABC中,∠ACB=90°,tan∠CAB=$\frac{\sqrt{3}}{3}$,AB=3,点D在以斜边AB为直径的半圆上,点M是CD的三等分点,当点D沿着半圆,从点A运动到点B时,点M运动的路径长为( )
如图,在Rt△ABC中,∠ACB=90°,tan∠CAB=$\frac{\sqrt{3}}{3}$,AB=3,点D在以斜边AB为直径的半圆上,点M是CD的三等分点,当点D沿着半圆,从点A运动到点B时,点M运动的路径长为( )| A. | π或$\frac{π}{2}$ | B. | $\frac{π}{2}$或$\frac{π}{3}$ | C. | $\frac{π}{3}$或π | D. | $\frac{π}{4}$或$\frac{π}{3}$ |
 如图,已知四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E,求证:四边形AMEN是菱形.
如图,已知四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E,求证:四边形AMEN是菱形.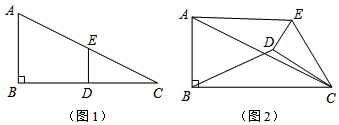
 如图,大楼AD与塔CB之间的距离AC长为27m,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D处测得塔顶B的仰角为30°,分别求大楼AD的高与塔BC的高(结果精确到0.1m,参考数据:$\sqrt{5}$≈2.24,$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
如图,大楼AD与塔CB之间的距离AC长为27m,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D处测得塔顶B的仰角为30°,分别求大楼AD的高与塔BC的高(结果精确到0.1m,参考数据:$\sqrt{5}$≈2.24,$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)