题目内容
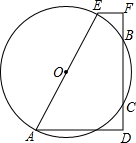 如图,梯形AEFD中,EF∥AD,∠F=90°,以AE为直径的⊙O交FD于B、C,若AD=3,BC=4,CD=1,求⊙O的直径.
如图,梯形AEFD中,EF∥AD,∠F=90°,以AE为直径的⊙O交FD于B、C,若AD=3,BC=4,CD=1,求⊙O的直径.考点:垂径定理,勾股定理,梯形中位线定理
专题:
分析:过点O作OM⊥BC,连结AB、BE、OB,先根据垂径定理得出CM的长,故可得出DM的长,再求出△ADB∽△BFE,由相似三角形的性质得出FE的长,由梯形中位线定理得出OM的长,根据勾股定理即可得出结论.
解答: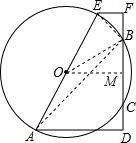 解:过点O作OM⊥BC,连结AB、BE、OB.
解:过点O作OM⊥BC,连结AB、BE、OB.
∵EF∥AD,点O是AE的中点,
∴FM=DM,BM=CM=2,
∴DM=2+1=3,即FM=3,BF=1.
∵AE是⊙O的直径,
∴∠ABE=90°,即∠FBE+∠DBA=90°.
∵∠F=90°,即FBE+∠BEF=90°,
∴∠ABD=∠BEF.
又∵∠F=∠D,
∴△ADB∽△BFE,
∴
=
,即
=
,解得FE=
.
∵OM是梯形的中位线,
∴OM=
(EF+AD)=
.
在Rt△OBM中OB2=OM2+BM2=(
)2+22=
,解得OB=
,即⊙O的直径为
.
 解:过点O作OM⊥BC,连结AB、BE、OB.
解:过点O作OM⊥BC,连结AB、BE、OB.∵EF∥AD,点O是AE的中点,
∴FM=DM,BM=CM=2,
∴DM=2+1=3,即FM=3,BF=1.
∵AE是⊙O的直径,
∴∠ABE=90°,即∠FBE+∠DBA=90°.
∵∠F=90°,即FBE+∠BEF=90°,
∴∠ABD=∠BEF.
又∵∠F=∠D,
∴△ADB∽△BFE,
∴
| AD |
| BF |
| DB |
| EF |
| 3 |
| 1 |
| 5 |
| EF |
| 5 |
| 3 |
∵OM是梯形的中位线,
∴OM=
| 1 |
| 2 |
| 7 |
| 3 |
在Rt△OBM中OB2=OM2+BM2=(
| 7 |
| 3 |
| 85 |
| 9 |
2
| ||
| 3 |
2
| ||
| 3 |
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出相似三角形是解答此题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
点P(2,-1)在反比例函数y=
(k≠0)的图象上,则k的值是( )
| -k |
| x |
| A、2 | ||
B、
| ||
| C、-2 | ||
D、-
|
 如图,已知点O在直线AB上,CO⊥DO于点O,若∠1=145°,则∠3的度数为( )
如图,已知点O在直线AB上,CO⊥DO于点O,若∠1=145°,则∠3的度数为( )| A、35° | B、45° |
| C、55° | D、65° |
 如图,在一张半透明的纸上画一条直线l,在l外任取一点Q,折出过点P且与l垂直的直线,这样的直线能折出几条?为什么?过点Q呢?
如图,在一张半透明的纸上画一条直线l,在l外任取一点Q,折出过点P且与l垂直的直线,这样的直线能折出几条?为什么?过点Q呢?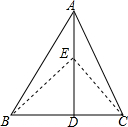 如图所示,在△ABC中,底边BC=8cm,高AD=6cm,点E为AD上一动点,当点E从点D附近向点A运动时,△BEC的面积发生了变化
如图所示,在△ABC中,底边BC=8cm,高AD=6cm,点E为AD上一动点,当点E从点D附近向点A运动时,△BEC的面积发生了变化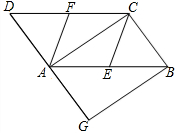 如图,在?ABCD中,E、F分别为边AB、CD的中点,AC是对角线,过点B作BG∥AC交DA的延长线于点G.
如图,在?ABCD中,E、F分别为边AB、CD的中点,AC是对角线,过点B作BG∥AC交DA的延长线于点G.