题目内容
2.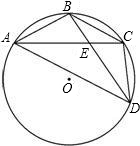 如图,已知A,B,C,D是⊙O上的四个点,AB=BC,BD交AC于点E,连接CD、AD.若BE=3,ED=6,则AB=3$\sqrt{3}$.
如图,已知A,B,C,D是⊙O上的四个点,AB=BC,BD交AC于点E,连接CD、AD.若BE=3,ED=6,则AB=3$\sqrt{3}$.
分析 等弦对等角可证DB平分∠ABC,证得△ABE∽△DBA,根据相似三角形的性质可求AB的长.
解答 解:∵AB=BC,
∴$\widehat{AB}$=$\widehat{BC}$,
∴∠BDC=∠ADB,
∴又∵∠ABE=∠ABD,
∴△ABE∽△DBA,
∴$\frac{AB}{BE}$=$\frac{BD}{AB}$,
∵BE=3,ED=6,
∴BD=9,
∴AB2=BE•BD=3×9=27,
∴AB=3$\sqrt{3}$.
故答案为:3$\sqrt{3}$.
点评 此题考查相似三角形的判定与性质,圆周角定理,利用圆周角定理得出角相等,证得三角形相似是解决问题的关键.

练习册系列答案
相关题目
13.-5的绝对值是( )
| A. | -5 | B. | 5 | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
17.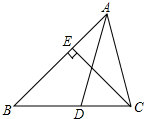 如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,则∠ADB的度数为( )
如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,则∠ADB的度数为( )
 如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,则∠ADB的度数为( )
如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,则∠ADB的度数为( )| A. | 40° | B. | 60° | C. | 80° | D. | 100° |
11. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:DF•DE=CE•CB;
(2)若AB=4,AD=3,AE=3,求AF的长.
 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.(1)求证:DF•DE=CE•CB;
(2)若AB=4,AD=3,AE=3,求AF的长.
12.代数式-3x2y,0,6x+y,$\frac{x+y}{4}$,$\frac{b}{a}$中,单项式的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,菱形ABCD中,AD∥BC,已知BC=CD=5,AC=8,求BD的长.
如图,菱形ABCD中,AD∥BC,已知BC=CD=5,AC=8,求BD的长.