题目内容
17.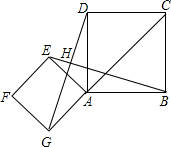 如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.(1)求证:EB=GD且EB⊥GD;
(2)若AB=2,AG=$\sqrt{2}$,求EB的长度.
分析 (1)在△GAD和△EAB中,∠GAD=90°+∠EAD,∠EAB=90°+∠EAD,得到∠GAD=∠EAB从而△GAD≌△EAB,即EB=GD;由∠AEB=∠AGD,∠EOH=∠AOG,即可得出∠EHG=∠EAG=90°;
(2)设BD与AC交于点O,由AB=AD=2在Rt△ABD中求得DB,利用勾股定理即可求得结果.
解答 证明:(1)如图1,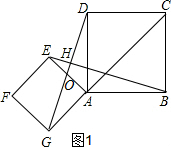
在△GAD和△EAB中,∠GAD=90°+∠EAD,∠EAB=90°+∠EAD
∴∠GAD=∠EAB,
∵四边形EFGA和四边形ABCD是正方形,
∴AG=AE,AB=AD,
在△GAD和△EAB中
$\left\{\begin{array}{l}{AB=AD}\\{∠EAB=∠GAD}\\{AE=AG}\end{array}\right.$,
∴△GAD≌△EAB(SAS),
∴EB=GD;∠AEB=∠AGD,
∵∠EOH=∠AOG,
∴∠EHG=∠EAG=90°,
∴EB=GD且EB⊥GD;
(2)如图2,连接BD,BD与AC交于点O,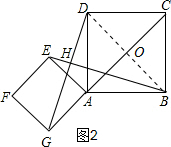
∵AB=AD=2,在Rt△ABD中,DB=$\sqrt{A{B}^{2}+A{D}^{2}}$=2$\sqrt{2}$,
∴AO=$\sqrt{2}$,
∴OG=OA+AG=$\sqrt{2}$+$\sqrt{2}$=2$\sqrt{2}$,
∴EB=GD=$\sqrt{O{G}^{2}+O{D}^{2}}$=$\sqrt{8+2}$=$\sqrt{10}$.
点评 本题考查了正方形的性质及全等三角形的判定与性质,利用三角形全等是解题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
14.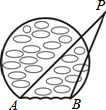 如图,两灯塔A、B间的距离恰好为暗礁所在的圆的半径,要使船P不驶入暗礁区,则航行中应保持∠P( )
如图,两灯塔A、B间的距离恰好为暗礁所在的圆的半径,要使船P不驶入暗礁区,则航行中应保持∠P( )
 如图,两灯塔A、B间的距离恰好为暗礁所在的圆的半径,要使船P不驶入暗礁区,则航行中应保持∠P( )
如图,两灯塔A、B间的距离恰好为暗礁所在的圆的半径,要使船P不驶入暗礁区,则航行中应保持∠P( )| A. | 大于60° | B. | 大于30° | C. | 小于60° | D. | 小于30° |
9.在某次赈灾晚会中共募得善款21.75亿元,它用科学记数法可表示为( )
| A. | 2.175×106元 | B. | 2.175×107元 | C. | 2.175×108元 | D. | 2.175×109元 |
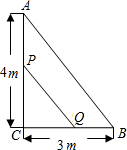 如图所示,在Rt△ABC中,点P,Q同时由A,B两点出发分别沿射线AC,BC方向匀速运动,其速度均为2cm/s,当△PCQ的面积是△ABC的面积的一半时,所用的时间为3或0.5s.
如图所示,在Rt△ABC中,点P,Q同时由A,B两点出发分别沿射线AC,BC方向匀速运动,其速度均为2cm/s,当△PCQ的面积是△ABC的面积的一半时,所用的时间为3或0.5s.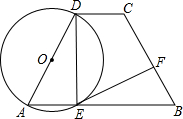 如图、在梯形ABCD中,AB∥CD,AD=BC,以AD为直径的⊙O交AB于E,过E作
如图、在梯形ABCD中,AB∥CD,AD=BC,以AD为直径的⊙O交AB于E,过E作 已知如图:在△ABC中,AD⊥BC于D,∠B=30°,∠C=45°,BD=2$\sqrt{3}$,求AC的长.
已知如图:在△ABC中,AD⊥BC于D,∠B=30°,∠C=45°,BD=2$\sqrt{3}$,求AC的长. 如图,△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,F在DE的延长线上,且AF=CE.
如图,△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,F在DE的延长线上,且AF=CE.