题目内容
12.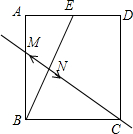 如图,矩形纸片ABCD中,点E是AD的中点,且AE=1,连接BE,分别以B、E为圆心,以大于$\frac{1}{2}BE$的长为半径作弧,两弧交于点M、N,若直线MN恰好过点C,则AB的长度为( )
如图,矩形纸片ABCD中,点E是AD的中点,且AE=1,连接BE,分别以B、E为圆心,以大于$\frac{1}{2}BE$的长为半径作弧,两弧交于点M、N,若直线MN恰好过点C,则AB的长度为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2 |
分析 如图,连接EC由FC垂直平分BE,得到∠BFC=∠EFC=90°,EF=BF,由于FC=FC,推出△BFC≌△CEF(SAS),于是得到BC=EC利用勾股定理可得AB=CD=$\sqrt{3}$.
解答 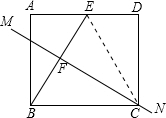 解:如图,连接EC
解:如图,连接EC
∵FC垂直平分BE,即∠BFC=∠EFC=90°,EF=BF,
又∵FC=FC,
在△BFC与△CEF中$\left\{\begin{array}{l}{EF=BF}\\{∠BFC=∠EFC}\\{FC=FC}\end{array}\right.$,
∴△BFC≌△CEF(SAS),
∴BC=EC
又∵AD=BC,AE=1
故EC=2
利用勾股定理可得AB=CD=$\sqrt{3}$.
故选B.
点评 本题考查的是线段垂直平分线的性质以及矩形的性质,本题的关键是要画出辅助线,证明三角形全等后易求解.本题难度中等.

练习册系列答案
相关题目
17.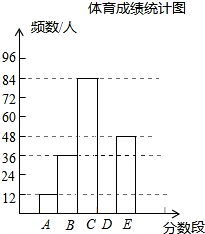 为了了解某市初三年级学生体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:25.5~30.5;B:30.5~35.5;C:35.5~40.5;D:40.5~45.5;E:45.5~50.5)统计如下:
为了了解某市初三年级学生体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:25.5~30.5;B:30.5~35.5;C:35.5~40.5;D:40.5~45.5;E:45.5~50.5)统计如下:
体育成绩统计表
根据上面提供的信息,回答下列问题:
(1)在统计表中,a=0.15,b=60,并将统计图补充完整;
(2)小明说:“这组数据的中位数一定在C中.”你认为小明的说法正确吗?正确(填“正确”或“错误”);
(3)若成绩在40分以上(含40分)定为优秀,则该市今年48000名初三年级学生中体育成绩为优秀的学生人数约有多少?
 为了了解某市初三年级学生体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:25.5~30.5;B:30.5~35.5;C:35.5~40.5;D:40.5~45.5;E:45.5~50.5)统计如下:
为了了解某市初三年级学生体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:25.5~30.5;B:30.5~35.5;C:35.5~40.5;D:40.5~45.5;E:45.5~50.5)统计如下:体育成绩统计表
| 分数段 | 频数/人 | 频率 |
| A | 12 | 0.05 |
| B | 36 | a |
| C | 84 | 0.35 |
| D | b | 0.25 |
| E | 48 | 0.20 |
(1)在统计表中,a=0.15,b=60,并将统计图补充完整;
(2)小明说:“这组数据的中位数一定在C中.”你认为小明的说法正确吗?正确(填“正确”或“错误”);
(3)若成绩在40分以上(含40分)定为优秀,则该市今年48000名初三年级学生中体育成绩为优秀的学生人数约有多少?
1.在直角三角形中,各边的长度都扩大3倍,则锐角A的三角函数值( )
| A. | 扩大3倍 | B. | 缩小为原来的$\frac{1}{3}$ | C. | 都不变 | D. | 无法确定 |
1.二次函数y=x2-5x+3的一组对应值如表所示:
请你判断方程x2-5x+3=0的一个解x的近似值为4.3(精确到0.1).
| x | 4.1 | 4.2 | 4.3 | 4.4 |
| y | -0.69 | -0.36 | -0.01 | 0.35 |
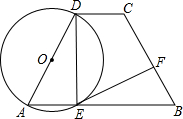 如图、在梯形ABCD中,AB∥CD,AD=BC,以AD为直径的⊙O交AB于E,过E作
如图、在梯形ABCD中,AB∥CD,AD=BC,以AD为直径的⊙O交AB于E,过E作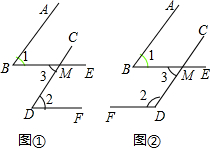 已知一个角的两边与另一个角的两边分别平行,请结合图,探索这两个角之间的关系,并说明理由.
已知一个角的两边与另一个角的两边分别平行,请结合图,探索这两个角之间的关系,并说明理由. 如图,△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,F在DE的延长线上,且AF=CE.
如图,△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,F在DE的延长线上,且AF=CE.