题目内容
18．在同一平面内，直线a、b、c中，若a⊥b，b∥c，则a、c的位置关系是c⊥a．分析 根据b∥c，则得到同旁内角互补，然后利用a⊥b即可得到a与c的夹角为90度，则可判断a⊥c．
解答 解：∵c∥b，a⊥b，
∴c⊥a．
故答案为c⊥a
点评 本题考查了平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．
练习册系列答案
相关题目
8．
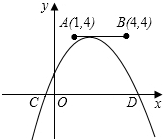如图，点A，B的坐标分别为（1，4）和（4，4），抛物线y=a（x-m）2+n的顶点在线段AB上运动，与x轴交于C、D两点（C在D的左侧），点C的横坐标最小值为-3，则点D的横坐标最大值为（ ）
如图，点A，B的坐标分别为（1，4）和（4，4），抛物线y=a（x-m）2+n的顶点在线段AB上运动，与x轴交于C、D两点（C在D的左侧），点C的横坐标最小值为-3，则点D的横坐标最大值为（ ）| A． | 13 | B． | 7 | C． | 5 | D． | 8 |
9．使分式$\frac{（x+2）（x-2）}{（x+2）}$有意义的条件是（ ）
| A． | x≠0 | B． | x≠-2 | C． | x≠2 | D． | x可取任意实数 |
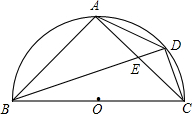如图，BC为半圆的直径，O为圆心，D是弧AD的中点，四边形ABCD的对角线AC、BD交于点E．求证：△ABE∽△DBC．
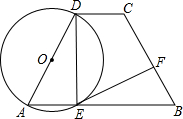如图、在梯形ABCD中，AB∥CD，AD=BC，以AD为直径的⊙O交AB于E，过E作