题目内容
 抛物线与直线y=m的交点,图中抛物线的解析式为y=ax2+bx+c,根据图象判断下列方程根的情况.
抛物线与直线y=m的交点,图中抛物线的解析式为y=ax2+bx+c,根据图象判断下列方程根的情况.(1)方程ax2+bx+c=0的两根分别为
(2)方程ax2+bx+c-3=0的两根分别为
(3)方程ax2+bx+c=2的根的情况是
(4)方程ax2+bx+c=4的根的情况是
考点:抛物线与x轴的交点
专题:
分析:直接根据抛物线与坐标轴及各直线的交点即可得出结论.
解答:解:(1)∵由图可知,抛物线与x轴有两个交点,且交点坐标为(-2.5,0),(0.5,0),
∴方程ax2+bx+c=0有两个不相等的实数根,且x1=-2.5,x2=0.5.
故答案为:x1=-2.5,x2=0.5;
(2))∵由图可知,抛物线与直线y=3有一个交点,且交点坐标为(-1,3),
∴方程ax2+bx+c-3=0有两个相等的实数根,且x1=x2=-1.
故答案为:x1=x2=-1;
(3)∵由图可知,抛物线与直线y=2有两个交点,
∴方程ax2+bx+c=2有两个不相等的实数根.
故答案为:两个不相等的实数根;
(4)∵由图可知,抛物线与直线y=4没有交点,
∴方程ax2+bx+c=4没有实数根.
故答案为:没有实数根.
∴方程ax2+bx+c=0有两个不相等的实数根,且x1=-2.5,x2=0.5.
故答案为:x1=-2.5,x2=0.5;
(2))∵由图可知,抛物线与直线y=3有一个交点,且交点坐标为(-1,3),
∴方程ax2+bx+c-3=0有两个相等的实数根,且x1=x2=-1.
故答案为:x1=x2=-1;
(3)∵由图可知,抛物线与直线y=2有两个交点,
∴方程ax2+bx+c=2有两个不相等的实数根.
故答案为:两个不相等的实数根;
(4)∵由图可知,抛物线与直线y=4没有交点,
∴方程ax2+bx+c=4没有实数根.
故答案为:没有实数根.
点评:本题考查的是抛物线与x轴的交点,能利用数形结合求出方程的根是解答此题的关键.

练习册系列答案
相关题目
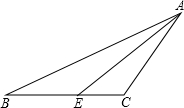 如图,在△ABC中,∠C-∠B=90°,AE是∠BAC的平分线,求∠AEC的度数.
如图,在△ABC中,∠C-∠B=90°,AE是∠BAC的平分线,求∠AEC的度数. 如图,梯形ABCD中.AB∥CD.且AB=2CD,E,F分别是AB,BC的中点.EF与BD相交于点M.
如图,梯形ABCD中.AB∥CD.且AB=2CD,E,F分别是AB,BC的中点.EF与BD相交于点M.