题目内容
17．观察下列数，根据规律写出横线上的数$\frac{1}{2}$，-$\frac{3}{4}$，$\frac{5}{8}$，-$\frac{7}{16}$，$\frac{9}{32}$，…第2010个数是-$\frac{4019}{{2}^{2010}}$．分析 分子为连续的奇数，分母是2的n次幂，奇数位置为正，偶数位置为负，由此得出第n个数为（-1）n+1$\frac{2n-1}{{2}^{n}}$，进一步代入求得答案即可．
解答 解：∵第n个数为（-1）n+1$\frac{2n-1}{{2}^{n}}$，
∴第5个数是$\frac{2×5-1}{{2}^{5}}$=$\frac{9}{32}$，第2010个数是-$\frac{2×2010-1}{{2}^{2010}}$=-$\frac{4019}{{2}^{2010}}$．
故答案为：$\frac{9}{32}$，-$\frac{4019}{{2}^{2010}}$．
点评 此题考查数字的变化规律，找出数字之间的联系，得出运算规律，利用规律解决问题．
练习册系列答案
应用题作业本系列答案
相关题目
汽车油箱中原有油50升，如果行驶中每小时用油5升，求油箱的油量y（单位：升）随行驶时间x（单位：时）变化的函数关系式，并写出自变量x的取值范围．
如图，在△ABC中，∠ACB=90°，在AC上取点D，使AD=BD，连结BD．若∠DBC=20°，求∠A的度数．
2．下列结论正确的是（ ）
| A． | 若a2=b2，则a=b | B． | 若a＞b，则a2＞b2 | ||
| C． | 若a≠0，b≠0，则a2+b2＞0 | D． | 若a≠b，则a2≠b2 |
如图，将一块长50厘米、宽40厘米的铁皮剪去四个正方形的角，就可以折成一个长方体无盖盒子．如果盒子的底面积为600平方厘米，求盒子的高度．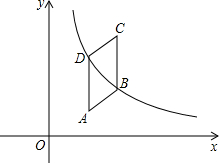
如图，在?ABCD中，AB⊥BD，sinA=$\frac{4}{5}$，将?ABCD放置在平面直角坐标系中，且AD⊥x轴，点D的横坐标为1，点C的纵坐标为3，恰有一条双曲线y=$\frac{k}{x}$（k＞0）同时经过B、D两点，则点B的坐标是（$\frac{9}{5}$，$\frac{4}{3}$）．