题目内容
初一(三)班体育委员统计了全班同学60秒跳绳次数,并列出下列频数分布表:
(1)全班有 名同学;
(2)组距是 ,组数是 ;
(3)跳绳次数x在100≤x<140范围的同学有 人,占全班同学 %;
(4)若使跳绳次数x在100≤x<140范围内的同学到初三毕业时占全班学生人数的87.12%,则初二、初三平均每年的增长率为多少?
| 次数 | 60≤x<80 | 80≤x<100 | 100≤x<120 | 120≤x<14 | 140≤x<160 |
160≤x<180 |
| 频数 | 1 | 4 | 21 | 15 | 5 | 4 |
(2)组距是
(3)跳绳次数x在100≤x<140范围的同学有
(4)若使跳绳次数x在100≤x<140范围内的同学到初三毕业时占全班学生人数的87.12%,则初二、初三平均每年的增长率为多少?
考点:一元二次方程的应用,频数(率)分布表
专题:
分析:(1)由图可知所有的频数之和即为人数;
(2)由频数分布表可知组距为20,组数为6;
(3)将第三组与第四组的频数相加即可得出跳绳次数在100≤x<140范围的同学人数,再利用公式
×100%计算即可;
(4)设初二、初三平均每年的增长率为x,根据题意列出方程36(1+x)2=50×87.12%,解方程即可.
(2)由频数分布表可知组距为20,组数为6;
(3)将第三组与第四组的频数相加即可得出跳绳次数在100≤x<140范围的同学人数,再利用公式
| 频数 |
| 总数 |
(4)设初二、初三平均每年的增长率为x,根据题意列出方程36(1+x)2=50×87.12%,解方程即可.
解答:解:(1)全班总人数=1+4+21+15+5+4=50(人);
(2)组距为20,组数为6;
(3)∵跳绳次数在100≤x<140范围的同学有多21+15=36人,
∴占全班的百分比=
×100%=72%;
(4)设初二、初三平均每年的增长率为x,由题意,得
36(1+x)2=50×87.12%,
1+x=±1.1,
x1=0.1=10% x2=-2.1(不合题意,舍去).
故答案为 50;20,6;36,72.
(2)组距为20,组数为6;
(3)∵跳绳次数在100≤x<140范围的同学有多21+15=36人,
∴占全班的百分比=
| 36 |
| 50 |
(4)设初二、初三平均每年的增长率为x,由题意,得
36(1+x)2=50×87.12%,
1+x=±1.1,
x1=0.1=10% x2=-2.1(不合题意,舍去).
故答案为 50;20,6;36,72.
点评:本题考查了一元二次方程的应用和频数分布表,频数分布表能够表示出具体数字,知道频率=频数÷总数和考查根据图表获取信息的能力.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
 如图,AD是△ABC的角平分线,DE∥AB交AC于点E,AB=8,AC=6,则DE=
如图,AD是△ABC的角平分线,DE∥AB交AC于点E,AB=8,AC=6,则DE= 如图,在△ABC中,D是AB边上一点,⊙O过D、B、C三点,∠DOC=2∠ACD=90°.
如图,在△ABC中,D是AB边上一点,⊙O过D、B、C三点,∠DOC=2∠ACD=90°.
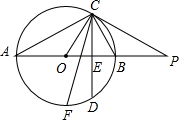 如图,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,∠COB=2∠PCB.
如图,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,∠COB=2∠PCB.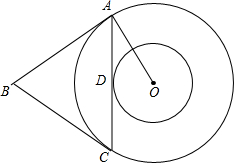 如图,△ABC的边AB、AC分别切大圆O于点A、C,边AC切小圆O于点D,CD=3,sinB=
如图,△ABC的边AB、AC分别切大圆O于点A、C,边AC切小圆O于点D,CD=3,sinB=