Question

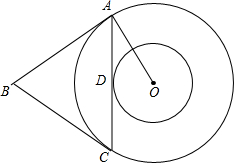如图，△ABC的边AB、AC分别切大圆O于点A、C，边AC切小圆O于点D，CD=3，sinB=

15

17

，若大圆O半径是R，小圆O半径是r，则(

5 34 R

3

-20r+1)2014=

 

．

Answer 1

考点：切线的性质

专题：

分析：过点A作AE⊥BC于E，设AE=15x，则AB=17x，BE=8x；在Rt△ACE中，可求出AB、AC的长度，再求出R．r的值，代入即可求出问题的答案．

解答：解：过点A作AE⊥BC于E，在Rt△ABE中，
由sinB=

15

17

，设AE=15x，则AB=17x，BE=8x；
在Rt△ACE中，AC=2CD=6，AE=15x，CE=9x，
求出x的值，并求出AB=BC=

34

；
连接OB，则点D在OB上，由射影定理求出R=

3 34

5

，r=

9

5

，
代入(

5 34 R

3

-20r+1)2014=1，
故答案为：1．

点评：本题考查了切线的性质、勾股定理的运用、相似三角形的判定和性质，解题的关键是正确的添加辅助线构造直角三角形，利用方程的思想解决几何图形问题．