题目内容
2.阅读理解材料:把分母中的根号去掉叫做分母有理化,例如:①$\frac{2}{{\sqrt{5}}}=\frac{{2\sqrt{5}}}{{\sqrt{5}•\sqrt{5}}}=\frac{{2\sqrt{5}}}{5}$;②$\frac{1}{{\sqrt{2}-1}}=\frac{{1×(\sqrt{2}+1)}}{{(\sqrt{2}-1)(\sqrt{2}+1)}}=\frac{{\sqrt{2}+1}}{{{{(\sqrt{2})}^2}-{1^2}}}=\sqrt{2}+1$等运算都是分母有理化.根据上述材料,
(1)化简:$\frac{1}{{\sqrt{3}-\sqrt{2}}}$;
(2)计算:$\frac{1}{{\sqrt{2}+1}}+\frac{1}{{\sqrt{3}+\sqrt{2}}}+\frac{1}{{\sqrt{4}+\sqrt{3}}}+…+\frac{1}{{\sqrt{2014}+\sqrt{2013}}}$.
分析 (1)根据二次根式的乘法,分子分母都乘以$\sqrt{3}+\sqrt{2}$,即可得出答案;
(2)根据分母有理化,可得实数的减法,根据实数的减法运算,可得答案.
解答 解:(1)原式=$\frac{1×(\sqrt{3}+\sqrt{2})}{(\sqrt{3}-\sqrt{2})(\sqrt{3}+\sqrt{2})}$=$\sqrt{3}+\sqrt{2}$;
(2)原式=$\frac{\sqrt{2}-1}{(\sqrt{2}+1)(\sqrt{2}-1)}$+$\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$+$\frac{\sqrt{4}-\sqrt{3}}{(\sqrt{4}+\sqrt{3})(\sqrt{4}-\sqrt{3})}$+…+$\frac{\sqrt{2014}-\sqrt{2013}}{(\sqrt{2014}+\sqrt{2013})(\sqrt{2014}-\sqrt{2013})}$
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{2014}-\sqrt{2013}$
=$\sqrt{2014}$-1.
点评 此题考查了二次根式的分母有理化,二次根式有理化主要利用了平方差公式,所以一般二次根式的有理化因式是符合平方差公式的特点的式子.即一项符号和绝对值相同,另一项符号相反绝对值相等.找出分母的有理化因式是解本题的关键.

练习册系列答案
相关题目
12.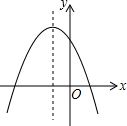 已知二次函数y=ax2+bx+c的图象如图所示,则点P(a,bc)在( )
已知二次函数y=ax2+bx+c的图象如图所示,则点P(a,bc)在( )
 已知二次函数y=ax2+bx+c的图象如图所示,则点P(a,bc)在( )
已知二次函数y=ax2+bx+c的图象如图所示,则点P(a,bc)在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图所示(单位:厘米),已知甲的面积是36平方厘米,乙的面积是45平方厘米,丙的面积是28平方厘米,则丁的面积是35平方厘米.
如图所示(单位:厘米),已知甲的面积是36平方厘米,乙的面积是45平方厘米,丙的面积是28平方厘米,则丁的面积是35平方厘米.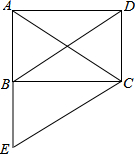 已知:如图,矩形ABCD的对角线AC、BD相交于点O,CE∥DB,交AB的延长线于点E.求证:AC=EC.
已知:如图,矩形ABCD的对角线AC、BD相交于点O,CE∥DB,交AB的延长线于点E.求证:AC=EC.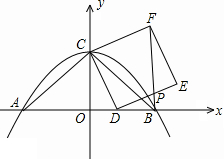 如图,抛物线y=-$\frac{1}{4}$x2+4交x轴于点A、B,交y轴于点C,连结AC,BC,D是线段OB上一动点,以CD为一边向右侧作正方形CDEF,连结BF,交DE于点P.
如图,抛物线y=-$\frac{1}{4}$x2+4交x轴于点A、B,交y轴于点C,连结AC,BC,D是线段OB上一动点,以CD为一边向右侧作正方形CDEF,连结BF,交DE于点P.