题目内容
10.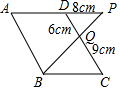 图中,ABCD为平行四边形,ADP、BQP及CQD均为直线.
图中,ABCD为平行四边形,ADP、BQP及CQD均为直线.(1)求证:△BCQ∽△PDQ;
(2)求四边形ABCD的周长.
分析 (1)由四边形ABCD是平行四边形知AP∥BC,据此得出∠QBC=∠QPD、∠QCB=∠QDP,即可证得△BCQ∽△PDQ;
(2)根据相似三角形的性质得出$\frac{BC}{PD}$=$\frac{CQ}{DQ}$即$\frac{BC}{8}$=$\frac{9}{6}$,求得BC的长,由周长公式求解可得.
解答 解:(1)∵四边形ABCD是平行四边形,
∴AP∥BC,
∴∠QBC=∠QPD、∠QCB=∠QDP,
∴△BCQ∽△PDQ;
(2)∵△BCQ∽△PDQ,
∴$\frac{BC}{PD}$=$\frac{CQ}{DQ}$,即$\frac{BC}{8}$=$\frac{9}{6}$,
解得:BC=12,
则四边形ABCD的周长为2(12+6+9)=54cm.
点评 本题主要考查相似三角形的判定与性质、平行四边形的性质,熟练掌握相似三角形的判定与性质是解题的关键.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
20.若关于x的一元二次方程为ax2+bx+5=0(a≠0)的解是x=1,则2013-a-b的值是( )
| A. | 2 018 | B. | 2 008 | C. | 2 014 | D. | 2 012 |
19. 如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm,则这只铅笔的长度可能是( )
如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm,则这只铅笔的长度可能是( )
 如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm,则这只铅笔的长度可能是( )
如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm,则这只铅笔的长度可能是( )| A. | 9cm | B. | 12cm | C. | 15cm | D. | 18cm |

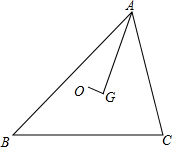 点O、G分别是△ABC的外心和重心,若AG⊥OG,求$\frac{A{B}^{2}+A{C}^{2}}{B{C}^{2}}$的值.
点O、G分别是△ABC的外心和重心,若AG⊥OG,求$\frac{A{B}^{2}+A{C}^{2}}{B{C}^{2}}$的值.
 如图,长为10cm的弹性皮筋直放置在直线l上,固定两端A和B,然后把中点C垂直向上拉升12cm至D点,则弹性皮筋被拉长了16cm.
如图,长为10cm的弹性皮筋直放置在直线l上,固定两端A和B,然后把中点C垂直向上拉升12cm至D点,则弹性皮筋被拉长了16cm.