题目内容
16.(1)解方程:$\frac{2x-3}{5}-\frac{x-2}{4}=-1$;(2)求不等式组$\left\{\begin{array}{l}\;2-3x>-2x\;\\ \;4+\frac{x}{2}>\frac{5}{2}\;.\end{array}\right.$的所有整数解.
分析 (1)首先去分母、然后去括号、移项、合并同类项、系数化成1即可求解;
(2)首先解不等式组,然后确定不等式组中的整数解即可.
解答 解:(1)去分母,得4(2x-3)-5(x-2)=-20,
去括号,得8x-12-5x+10=-20,
移项、合并同类项,得3x=-18,
系数化成1得x=-6.
(2)$\left\{\begin{array}{l}{2-3x>-2x…①}\\{4+\frac{x}{2}>\frac{5}{2}…②}\end{array}\right.$,
解不等式①,得x<2.解不等式②,得x>-3.
该不等式组的解集是:-3<x<2.
所有整数解为:-2,-1,0,1.
点评 此题考查的是一元一次不等式的解法和一元一次方程的解,根据x的取值范围,得出x的整数解,求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
相关题目
6. 如图所示,该几何体的主视图是( )
如图所示,该几何体的主视图是( )
 如图所示,该几何体的主视图是( )
如图所示,该几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
4. 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )
 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
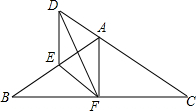 如图,△ABC中,AB=AC,F为BC的中点,D为CA延长线上一点,∠DFE=∠B.
如图,△ABC中,AB=AC,F为BC的中点,D为CA延长线上一点,∠DFE=∠B. 如图,△ABC中,DE∥BC,
如图,△ABC中,DE∥BC,



 如图,原来是重叠的两个直角三角形,将其中一个三角形沿BC方向平移BE的距离,就得到此图形,则图中阴影部分的面积为32.5.
如图,原来是重叠的两个直角三角形,将其中一个三角形沿BC方向平移BE的距离,就得到此图形,则图中阴影部分的面积为32.5.