题目内容
3．（1）计算：2×（-3）+4×（$\frac{1}{2}$）-1-20160；（2）解方程：$\frac{1}{x-1}$-1=0．
分析 （1）分别利用负指数幂的性质以及零指数幂的性质分别化简进而求出答案；
（2）首先移项，进而去分母解方程即可，再检验得出答案．
解答 解：（1）2×（-3）+4×（$\frac{1}{2}$）-1-20160
=-6+4×2-1
=1；
（2）原式可变为：$\frac{1}{x-1}$=1，
则x-1=1，
解得：x=2，
检验：当x=2时，x-1≠0，故x=2是原方程的根．
点评 此题主要考查了解分式方程以及实数运算，正确掌握分式方程的解法是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
13．弹簧挂上物体后会伸长，已知一弹簧的长度（cm）与所挂物体的质量（kg）之间的关系如下表：
（1）如果物体的质量为x kg，弹簧长度为y cm，根据上表写出y与x的关系式；
（2）当物体的质量为2.5kg时，根据（1）的关系式，求弹簧的长度；
（3）当弹簧的长度为17cm时，根据（1）的关系式，求弹簧所挂物体的质量．
| 所挂物体的质量（kg） | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 弹簧的长度（cm） | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 | 15.5 |
（2）当物体的质量为2.5kg时，根据（1）的关系式，求弹簧的长度；
（3）当弹簧的长度为17cm时，根据（1）的关系式，求弹簧所挂物体的质量．
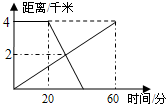已知A、B两地相距4km，上午8：00时，亮亮从A地步行到B地，8：20时芳芳从B地出发骑自行车到A地，亮亮和芳芳两人离A地的距离S（km）与亮亮所用时间t（min）之间的函数关系如图所示，下列四个说法中正确的有（ ）
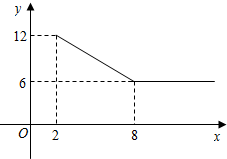某公司经营杨梅业务，以3万元/吨的价格买入杨梅后，分拣成A、B两类，A类杨梅包装后直接销售，包装成本为1万元/吨，它的平均销售价格y（单位：万元/吨）与销售数量x（x≥2，单位：吨）之间的函数关系如图所示；B类杨梅深加工后再销售，深加工总费用s（单位：万元）与加工数量t（单位：吨）之间的函数关系是s=12+3t，平均销售价格为9万元/吨．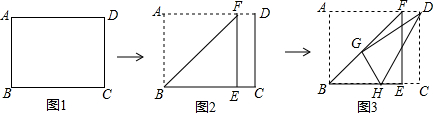
如图，已知AB是⊙O的直径，OD⊥AC，OD=3，则弦BC的长为6．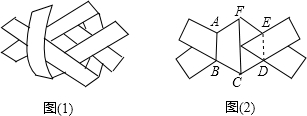
用两条宽均为2cm的纸条（假设纸条的长度足够长），折叠穿插，如图（1）所示，然后轻轻拉紧、压平就可以得到如图（2）所示的正六边形ABCDEF，则折出的正六边形的边长为$\frac{4\sqrt{3}}{3}$cm．