题目内容
1．
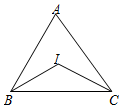如图，在△ABC中，∠A=66°，点I是内心，则∠BIC的大小为（ ）| A． | 114° | B． | 122° | C． | 123° | D． | 132° |
分析 根据三角形内角和定理求出∠ABC+∠ACB，根据内心的概念得到∠IBC=$\frac{1}{2}$∠ABC，∠ICB=$\frac{1}{2}$∠ACB，根据三角形内角和定理计算即可．
解答 解：∵∠A=66°，
∴∠ABC+∠ACB=114°，
∵点I是内心，
∴∠IBC=$\frac{1}{2}$∠ABC，∠ICB=$\frac{1}{2}$∠ACB，
∴∠IBC+∠ICB=57°，
∴∠BIC=180°-57°=123°，
故选：C．
点评 本题考查的是三角形的内切圆和内心，掌握三角形的内心的概念、三角形内角和定理是解题的关键．
练习册系列答案
相关题目
如图，∠1是五边形ABCDE的一个外角，若∠1=65°，则∠A+∠B+∠C+∠D=425°．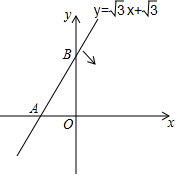
如图示直线y=$\sqrt{3}$x+$\sqrt{3}$与x轴、y轴分别交于点A、B，当直线绕着点A按顺时针方向旋转到与x轴首次重合时，点B运动的路径的长度为$\frac{2}{3}$π．
16．不等式-2x＞$\frac{1}{2}$的解集是（ ）
| A． | x＜-$\frac{1}{4}$ | B． | x＜-1 | C． | x＞-$\frac{1}{4}$ | D． | x＞-1 |
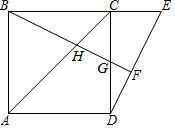如图，点E是正方形ABCD的边BC延长线上一点，连结DE，过顶点B作BF⊥DE，垂足为F，BF分别交AC于H，交CD于G．
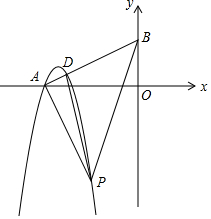已知抛物线C：y=（x+2）[t（x+1）-（x+3）]，其中-7≤t≤-2，且无论t取任何符合条件的实数，点A，P都在抛物线C 上．
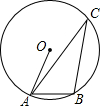如图，A，B，C是⊙O上的三点，若∠BAO=65°，则∠ACB的度数是25°．